Last updated: 2018-05-15

workflowr checks: (Click a bullet for more information)

  • ✔ R Markdown file: up-to-date

    Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

  • ✔ Environment: empty

    Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

  • ✔ Seed: set.seed(12345)

    The command set.seed(12345) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

  • ✔ Session information: recorded

    Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

  • ✔ Repository version: 388e65e

    Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility. The version displayed above was the version of the Git repository at the time these results were generated.

    Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated: 
    
Ignored files:
    Ignored:    .DS_Store
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/
    Ignored:    analysis/.DS_Store
    Ignored:    analysis/BH_robustness_cache/
    Ignored:    analysis/FDR_Null_cache/
    Ignored:    analysis/FDR_null_betahat_cache/
    Ignored:    analysis/Rmosek_cache/
    Ignored:    analysis/StepDown_cache/
    Ignored:    analysis/alternative2_cache/
    Ignored:    analysis/alternative_cache/
    Ignored:    analysis/ash_gd_cache/
    Ignored:    analysis/average_cor_gtex_2_cache/
    Ignored:    analysis/average_cor_gtex_cache/
    Ignored:    analysis/brca_cache/
    Ignored:    analysis/cash_deconv_cache/
    Ignored:    analysis/cash_fdr_1_cache/
    Ignored:    analysis/cash_fdr_2_cache/
    Ignored:    analysis/cash_fdr_3_cache/
    Ignored:    analysis/cash_fdr_4_cache/
    Ignored:    analysis/cash_fdr_5_cache/
    Ignored:    analysis/cash_fdr_6_cache/
    Ignored:    analysis/cash_plots_cache/
    Ignored:    analysis/cash_sim_1_cache/
    Ignored:    analysis/cash_sim_2_cache/
    Ignored:    analysis/cash_sim_3_cache/
    Ignored:    analysis/cash_sim_4_cache/
    Ignored:    analysis/cash_sim_5_cache/
    Ignored:    analysis/cash_sim_6_cache/
    Ignored:    analysis/cash_sim_7_cache/
    Ignored:    analysis/correlated_z_2_cache/
    Ignored:    analysis/correlated_z_3_cache/
    Ignored:    analysis/correlated_z_cache/
    Ignored:    analysis/create_null_cache/
    Ignored:    analysis/cutoff_null_cache/
    Ignored:    analysis/design_matrix_2_cache/
    Ignored:    analysis/design_matrix_cache/
    Ignored:    analysis/diagnostic_ash_cache/
    Ignored:    analysis/diagnostic_correlated_z_2_cache/
    Ignored:    analysis/diagnostic_correlated_z_3_cache/
    Ignored:    analysis/diagnostic_correlated_z_cache/
    Ignored:    analysis/diagnostic_plot_2_cache/
    Ignored:    analysis/diagnostic_plot_cache/
    Ignored:    analysis/efron_leukemia_cache/
    Ignored:    analysis/fitting_normal_cache/
    Ignored:    analysis/gaussian_derivatives_2_cache/
    Ignored:    analysis/gaussian_derivatives_3_cache/
    Ignored:    analysis/gaussian_derivatives_4_cache/
    Ignored:    analysis/gaussian_derivatives_5_cache/
    Ignored:    analysis/gaussian_derivatives_cache/
    Ignored:    analysis/gd-ash_cache/
    Ignored:    analysis/gd_delta_cache/
    Ignored:    analysis/gd_lik_2_cache/
    Ignored:    analysis/gd_lik_cache/
    Ignored:    analysis/gd_w_cache/
    Ignored:    analysis/knockoff_10_cache/
    Ignored:    analysis/knockoff_2_cache/
    Ignored:    analysis/knockoff_3_cache/
    Ignored:    analysis/knockoff_4_cache/
    Ignored:    analysis/knockoff_5_cache/
    Ignored:    analysis/knockoff_6_cache/
    Ignored:    analysis/knockoff_7_cache/
    Ignored:    analysis/knockoff_8_cache/
    Ignored:    analysis/knockoff_9_cache/
    Ignored:    analysis/knockoff_cache/
    Ignored:    analysis/knockoff_var_cache/
    Ignored:    analysis/marginal_z_alternative_cache/
    Ignored:    analysis/marginal_z_cache/
    Ignored:    analysis/mosek_reg_2_cache/
    Ignored:    analysis/mosek_reg_4_cache/
    Ignored:    analysis/mosek_reg_5_cache/
    Ignored:    analysis/mosek_reg_6_cache/
    Ignored:    analysis/mosek_reg_cache/
    Ignored:    analysis/pihat0_null_cache/
    Ignored:    analysis/plot_diagnostic_cache/
    Ignored:    analysis/poster_obayes17_cache/
    Ignored:    analysis/real_data_simulation_2_cache/
    Ignored:    analysis/real_data_simulation_3_cache/
    Ignored:    analysis/real_data_simulation_4_cache/
    Ignored:    analysis/real_data_simulation_5_cache/
    Ignored:    analysis/real_data_simulation_cache/
    Ignored:    analysis/rmosek_primal_dual_2_cache/
    Ignored:    analysis/rmosek_primal_dual_cache/
    Ignored:    analysis/seqgendiff_cache/
    Ignored:    analysis/simulated_correlated_null_2_cache/
    Ignored:    analysis/simulated_correlated_null_3_cache/
    Ignored:    analysis/simulated_correlated_null_cache/
    Ignored:    analysis/simulation_real_se_2_cache/
    Ignored:    analysis/simulation_real_se_cache/
    Ignored:    analysis/smemo_2_cache/
    Ignored:    data/LSI/
    Ignored:    docs/.DS_Store
    Ignored:    docs/figure/.DS_Store
    Ignored:    output/fig/
    Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
Expand here to see past versions:
    File Version Author Date Message
    html e05bc83 LSun 2018-05-12 Update to 1.0
    rmd cc0ab83 Lei Sun 2018-05-11 update
    html 0f36d99 LSun 2017-12-21 Build site.
    html 853a484 LSun 2017-11-07 Build site.
    rmd 7fe3699 LSun 2017-06-17 semicircular
    html 7fe3699 LSun 2017-06-17 semicircular

Data generation

Let \(L_{n \times k} = \left[L_{ij}\right]_{n \times k}\) be a matrix, each entry of which is generated as follows.

  1. Let \(L_{ij} \sim N(0, 1)\) independently.
  2. Let \(L_{ij} = \displaystyle\frac {L_{ij}}{\sqrt{L_{i1}^2 + \cdots + L_{ik}^2}}\). That is, normalizing each row so that each row has a unit \(l_2\) norm.

Then taking \(L\) as known, let \(x \sim N\left(0, I_k\right)\) be a \(k\)-dimensional vector comprised of \(k\) independent \(N\left(0, 1\right)\) random variables. Then \[ z = Lx \sim N\left(0, LL^T\right) \] should be \(n\) marginally \(N\left(0, 1\right)\) but correlated \(z\) scores. Indeed, \[ \begin{array}{c} \text{var}\left(z_i\right) = l_i^Tl_i = 1 \ ; \\ \text{cov}\left(z_i, z_j\right) = l_i^Tl_j \neq 0 \text{, in general} \ ; \end{array} \] where \(l_i^T\) and \(l_j^T\) are \(i^\text{th}\) and \(j^\text{th}\) rows of \(L\) respectively.

Then we plot the histogram of \(n\) \(z\) scores. One interesting thing is we can prove what these histograms would look like when \(n\) is sufficiently large.

\(k = 4\)

For example, when \(k = 4\), \(n\) is sufficiently large, say, \(10^6\), the histogram of \(z\) looks like a semicircle almost perfectly, as illustrated in the following simulation. The semicircle is centered at the origin, and has a radius of \(\left\|x\right\|_2\).

set.seed(1)
n = 1e6
k = 4
L = matrix(rnorm(n * k), nrow = n)
s = sqrt(rowSums(L^2))
L = L / s
x = rnorm(k)
z = L %*% x
hist(z, breaks = 100, prob = TRUE)
R = sqrt(sum(x^2))
x.plot = seq(-max(abs(z)) - 1, max(abs(z)) + 1, length = 1000)
y.plot = 2 * sqrt(pmax(R^2 - x.plot^2, 0)) / (pi * R^2)
lines(x.plot, y.plot, col = "red")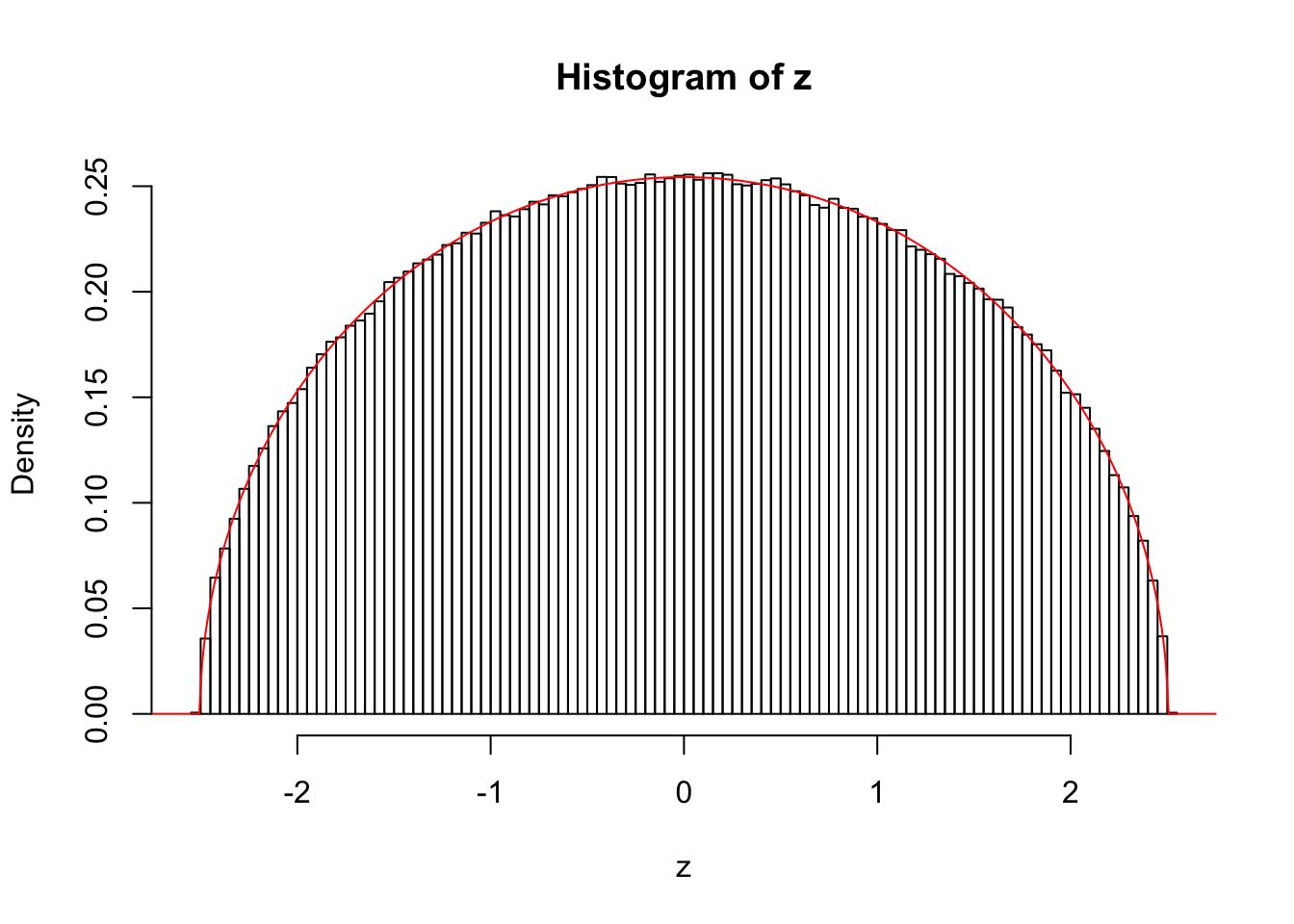

Expand here to see past versions of unnamed-chunk-1-1.png:
Version Author Date
0f36d99 LSun 2017-12-21
7fe3699 LSun 2017-06-17

Actually, when \(k \neq 4\), for example, \(k = 3\) or \(k = 5\), the histograms of these correlated \(z\) scores, simulated the same way, look different, and their shapes when \(n \to \infty\) can be mathematically determined.

\(k = 3\)

set.seed(1)
n = 1e6
k = 3
L = matrix(rnorm(n * k), nrow = n)
s = sqrt(rowSums(L^2))
L = L / s
x = rnorm(k)
z = L %*% x
hist(z, breaks = 100, prob = TRUE)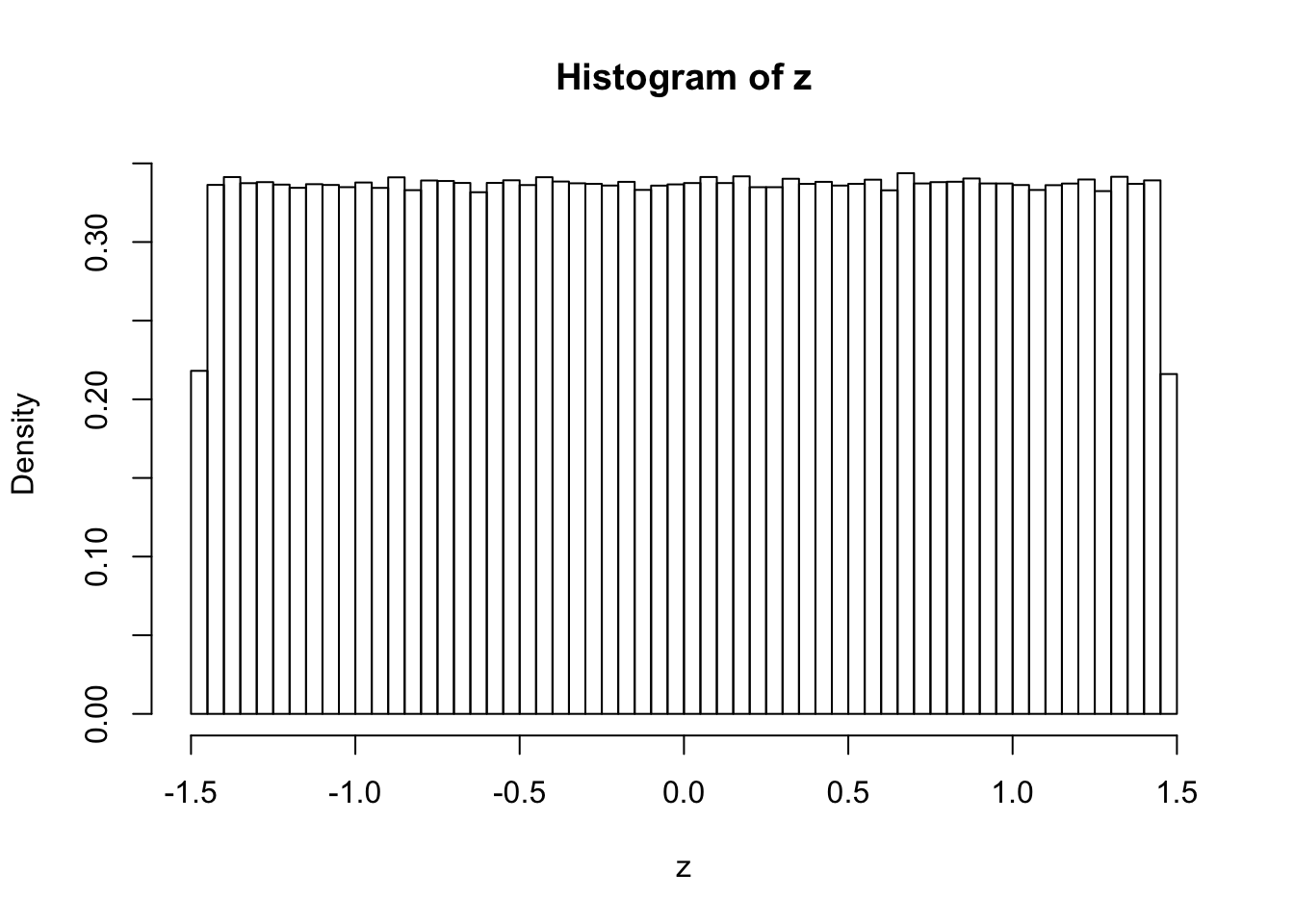

Expand here to see past versions of unnamed-chunk-2-1.png:
Version Author Date
0f36d99 LSun 2017-12-21
7fe3699 LSun 2017-06-17

\(k = 5\)

set.seed(1)
n = 1e6
k = 5
L = matrix(rnorm(n * k), nrow = n)
s = sqrt(rowSums(L^2))
L = L / s
x = rnorm(k)
z = L %*% x
hist(z, breaks = 100, prob = TRUE)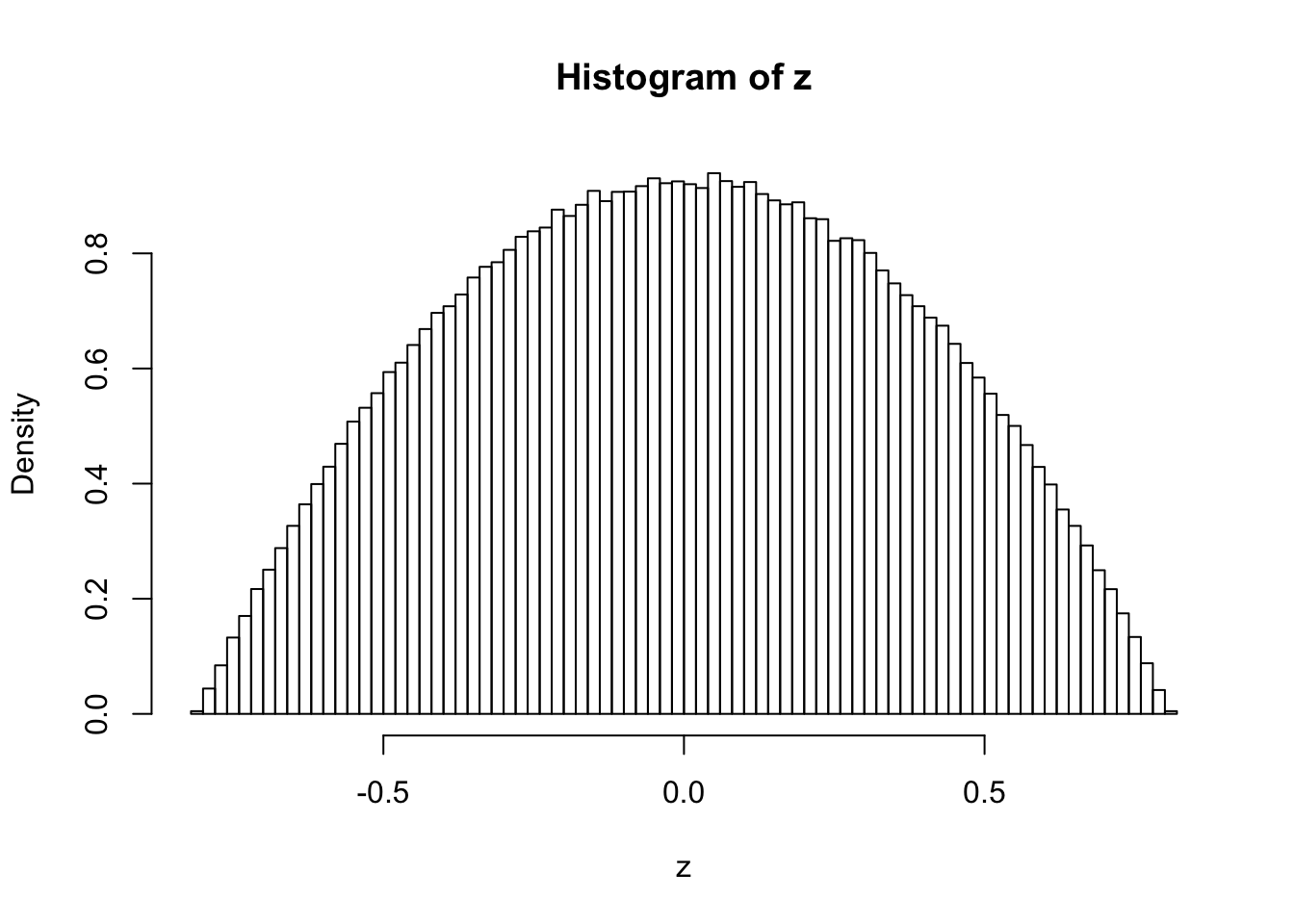

Expand here to see past versions of unnamed-chunk-3-1.png:
Version Author Date
0f36d99 LSun 2017-12-21
7fe3699 LSun 2017-06-17

Session information

sessionInfo()
R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.4

Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

loaded via a namespace (and not attached):
 [1] workflowr_1.0.1   Rcpp_0.12.16      digest_0.6.15    
 [4] rprojroot_1.3-2   R.methodsS3_1.7.1 backports_1.1.2  
 [7] git2r_0.21.0      magrittr_1.5      evaluate_0.10.1  
[10] stringi_1.1.6     whisker_0.3-2     R.oo_1.21.0      
[13] R.utils_2.6.0     rmarkdown_1.9     tools_3.4.3      
[16] stringr_1.3.0     yaml_2.1.18       compiler_3.4.3   
[19] htmltools_0.3.6   knitr_1.20

This reproducible R Markdown analysis was created with workflowr 1.0.1