Creating Null
Lei Sun
2017-05-08
Last updated: 2018-06-01
workflowr checks: (Click a bullet for more information)-
✔ R Markdown file: up-to-date
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
-
✔ Environment: empty
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
-
✔ Seed:
set.seed(12345)The command
set.seed(12345)was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible. -
✔ Session information: recorded
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
-
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility. The version displayed above was the version of the Git repository at the time these results were generated.✔ Repository version: 4cf3706
Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can usewflow_publishorwflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.Ignored files: Ignored: .DS_Store Ignored: .Rhistory Ignored: .Rproj.user/ Ignored: analysis/.DS_Store Ignored: analysis/BH_robustness_cache/ Ignored: analysis/FDR_Null_cache/ Ignored: analysis/FDR_null_betahat_cache/ Ignored: analysis/Rmosek_cache/ Ignored: analysis/StepDown_cache/ Ignored: analysis/alternative2_cache/ Ignored: analysis/alternative_cache/ Ignored: analysis/ash_gd_cache/ Ignored: analysis/average_cor_gtex_2_cache/ Ignored: analysis/average_cor_gtex_cache/ Ignored: analysis/brca_cache/ Ignored: analysis/cash_deconv_cache/ Ignored: analysis/cash_fdr_1_cache/ Ignored: analysis/cash_fdr_2_cache/ Ignored: analysis/cash_fdr_3_cache/ Ignored: analysis/cash_fdr_4_cache/ Ignored: analysis/cash_fdr_5_cache/ Ignored: analysis/cash_fdr_6_cache/ Ignored: analysis/cash_plots_2_cache/ Ignored: analysis/cash_plots_cache/ Ignored: analysis/cash_sim_1_cache/ Ignored: analysis/cash_sim_2_cache/ Ignored: analysis/cash_sim_3_cache/ Ignored: analysis/cash_sim_4_cache/ Ignored: analysis/cash_sim_5_cache/ Ignored: analysis/cash_sim_6_cache/ Ignored: analysis/cash_sim_7_cache/ Ignored: analysis/correlated_z_2_cache/ Ignored: analysis/correlated_z_3_cache/ Ignored: analysis/correlated_z_cache/ Ignored: analysis/create_null_cache/ Ignored: analysis/cutoff_null_cache/ Ignored: analysis/design_matrix_2_cache/ Ignored: analysis/design_matrix_cache/ Ignored: analysis/diagnostic_ash_cache/ Ignored: analysis/diagnostic_correlated_z_2_cache/ Ignored: analysis/diagnostic_correlated_z_3_cache/ Ignored: analysis/diagnostic_correlated_z_cache/ Ignored: analysis/diagnostic_plot_2_cache/ Ignored: analysis/diagnostic_plot_cache/ Ignored: analysis/efron_leukemia_cache/ Ignored: analysis/figure/ Ignored: analysis/fitting_normal_cache/ Ignored: analysis/gaussian_derivatives_2_cache/ Ignored: analysis/gaussian_derivatives_3_cache/ Ignored: analysis/gaussian_derivatives_4_cache/ Ignored: analysis/gaussian_derivatives_5_cache/ Ignored: analysis/gaussian_derivatives_cache/ Ignored: analysis/gd-ash_cache/ Ignored: analysis/gd_delta_cache/ Ignored: analysis/gd_lik_2_cache/ Ignored: analysis/gd_lik_cache/ Ignored: analysis/gd_w_cache/ Ignored: analysis/knockoff_10_cache/ Ignored: analysis/knockoff_2_cache/ Ignored: analysis/knockoff_3_cache/ Ignored: analysis/knockoff_4_cache/ Ignored: analysis/knockoff_5_cache/ Ignored: analysis/knockoff_6_cache/ Ignored: analysis/knockoff_7_cache/ Ignored: analysis/knockoff_8_cache/ Ignored: analysis/knockoff_9_cache/ Ignored: analysis/knockoff_cache/ Ignored: analysis/knockoff_var_cache/ Ignored: analysis/marginal_z_alternative_cache/ Ignored: analysis/marginal_z_cache/ Ignored: analysis/mosek_reg_2_cache/ Ignored: analysis/mosek_reg_4_cache/ Ignored: analysis/mosek_reg_5_cache/ Ignored: analysis/mosek_reg_6_cache/ Ignored: analysis/mosek_reg_cache/ Ignored: analysis/pihat0_null_cache/ Ignored: analysis/plot_diagnostic_cache/ Ignored: analysis/poster_obayes17_cache/ Ignored: analysis/real_data_simulation_2_cache/ Ignored: analysis/real_data_simulation_3_cache/ Ignored: analysis/real_data_simulation_4_cache/ Ignored: analysis/real_data_simulation_5_cache/ Ignored: analysis/real_data_simulation_cache/ Ignored: analysis/rmosek_primal_dual_2_cache/ Ignored: analysis/rmosek_primal_dual_cache/ Ignored: analysis/seqgendiff_cache/ Ignored: analysis/simulated_correlated_null_2_cache/ Ignored: analysis/simulated_correlated_null_3_cache/ Ignored: analysis/simulated_correlated_null_cache/ Ignored: analysis/simulation_real_se_2_cache/ Ignored: analysis/simulation_real_se_cache/ Ignored: analysis/smemo_2_cache/ Ignored: data/LSI/ Ignored: docs/.DS_Store Ignored: docs/figure/.DS_Store Ignored: output/fig/ Unstaged changes: Modified: analysis/cash_plots_2.rmd Modified: analysis/gd_w.rmd
Expand here to see past versions:
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | 4cf3706 | LSun | 2018-06-01 | wflow_publish(“analysis/create_null.Rmd”) |
| html | b8d63a5 | LSun | 2018-06-01 | Build site. |
| Rmd | 83b5f17 | LSun | 2018-06-01 | wflow_publish(“analysis/create_null.Rmd”) |
| html | 4d653b1 | LSun | 2018-05-15 | Build site. |
| html | e05bc83 | LSun | 2018-05-12 | Update to 1.0 |
| Rmd | cc0ab83 | Lei Sun | 2018-05-11 | update |
| html | 0f36d99 | LSun | 2017-12-21 | Build site. |
| html | 853a484 | LSun | 2017-11-07 | Build site. |
| html | 043bf89 | LSun | 2017-11-05 | transfer |
| html | b141020 | LSun | 2017-05-09 | writeups |
| Rmd | 547e651 | LSun | 2017-05-09 | creating null |
Introduction
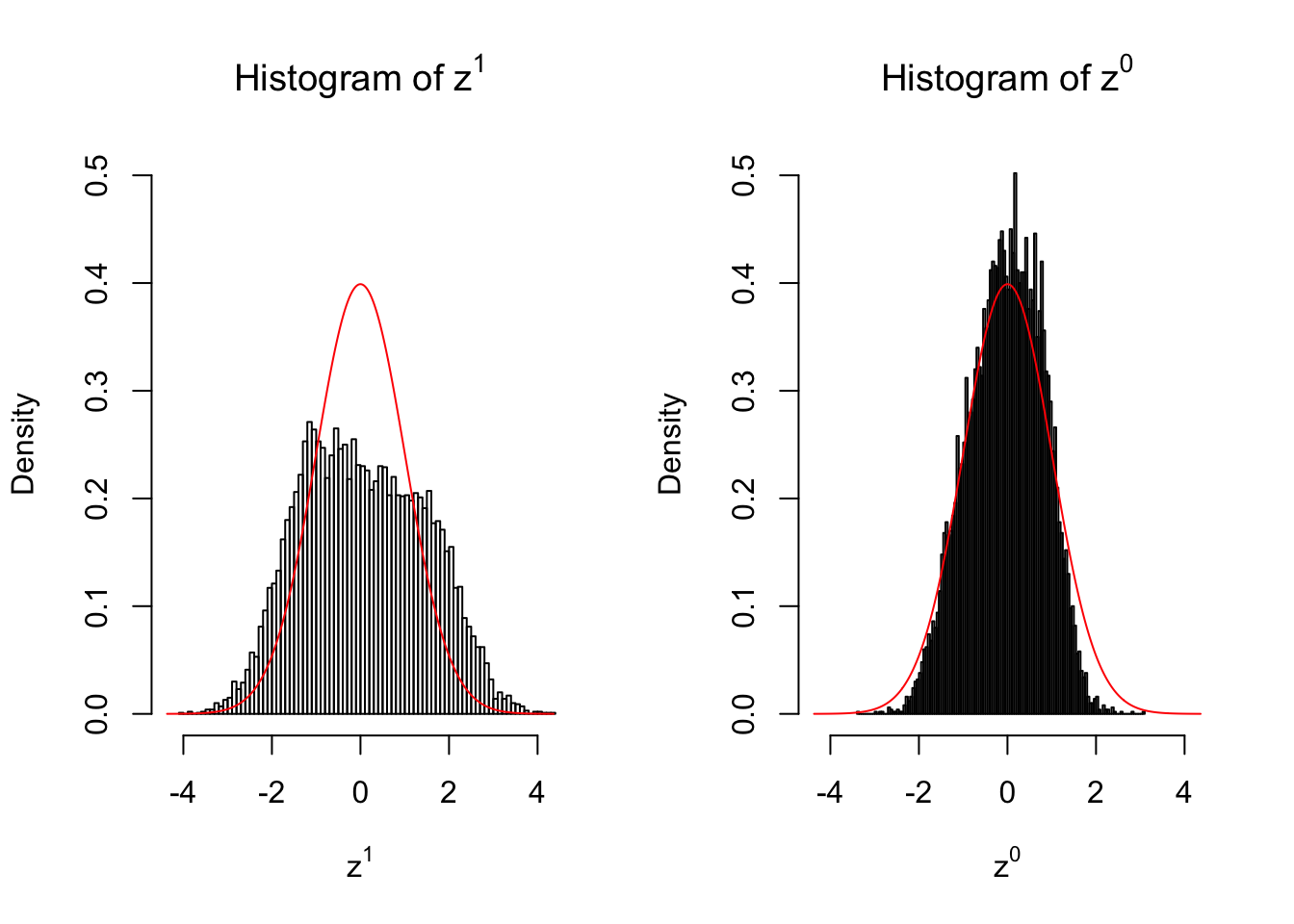
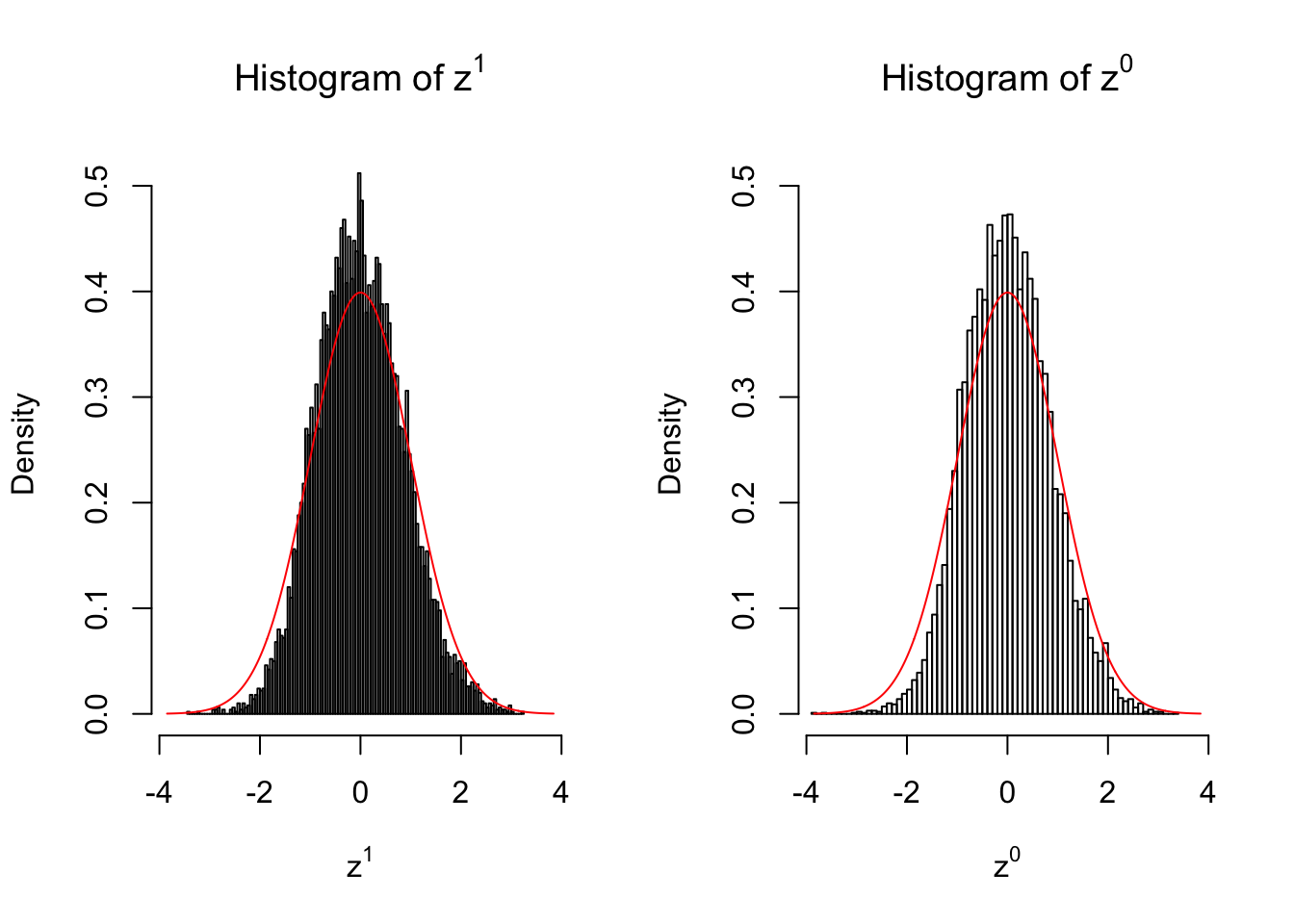
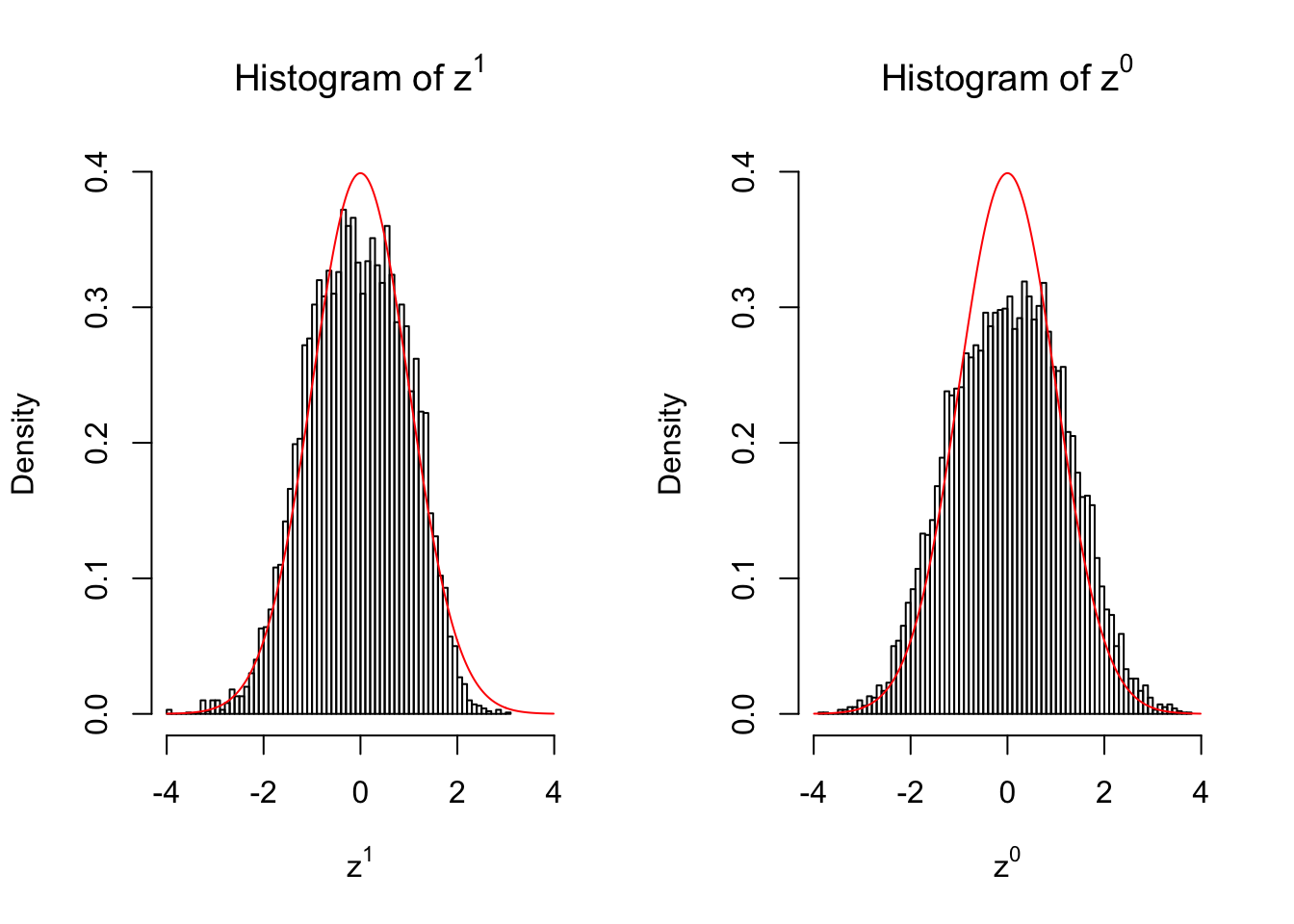
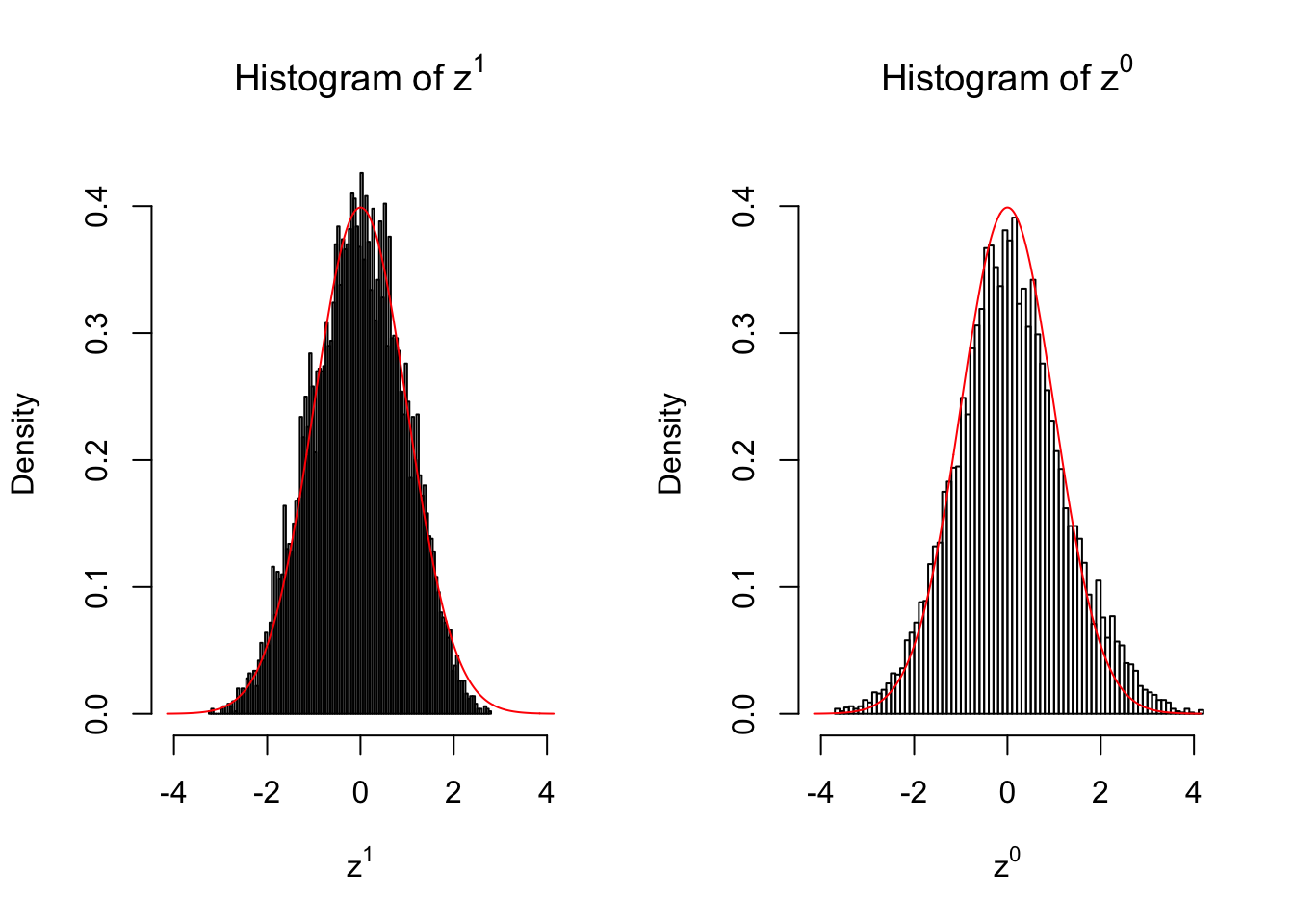
In many of his seminal papers on simultaneous inference, for example, Efron et al 2001, Efron used some techniques to create null from the raw data. One big concern of this approach is whether the created null could successfully remove the effects of interest whereas keep the distortion due to correlation. Let’s take a look.
Suppose in a simplified experiment, we have a data matrix \(X_{N \times 2n} = \left\{X_1, \ldots, X_n, X_{n + 1}, \ldots, X_{2n}\right\}\), \(n\) columns of which, \(\left\{X_1, \ldots, X_n\right\}\), are controls and \(n\) columns, \(\left\{X_{n + 1}, \ldots, X_{2n}\right\}\), are cases. We can obtain \(N\) \(z\) scores, called \(z^1\), from this experimental design.
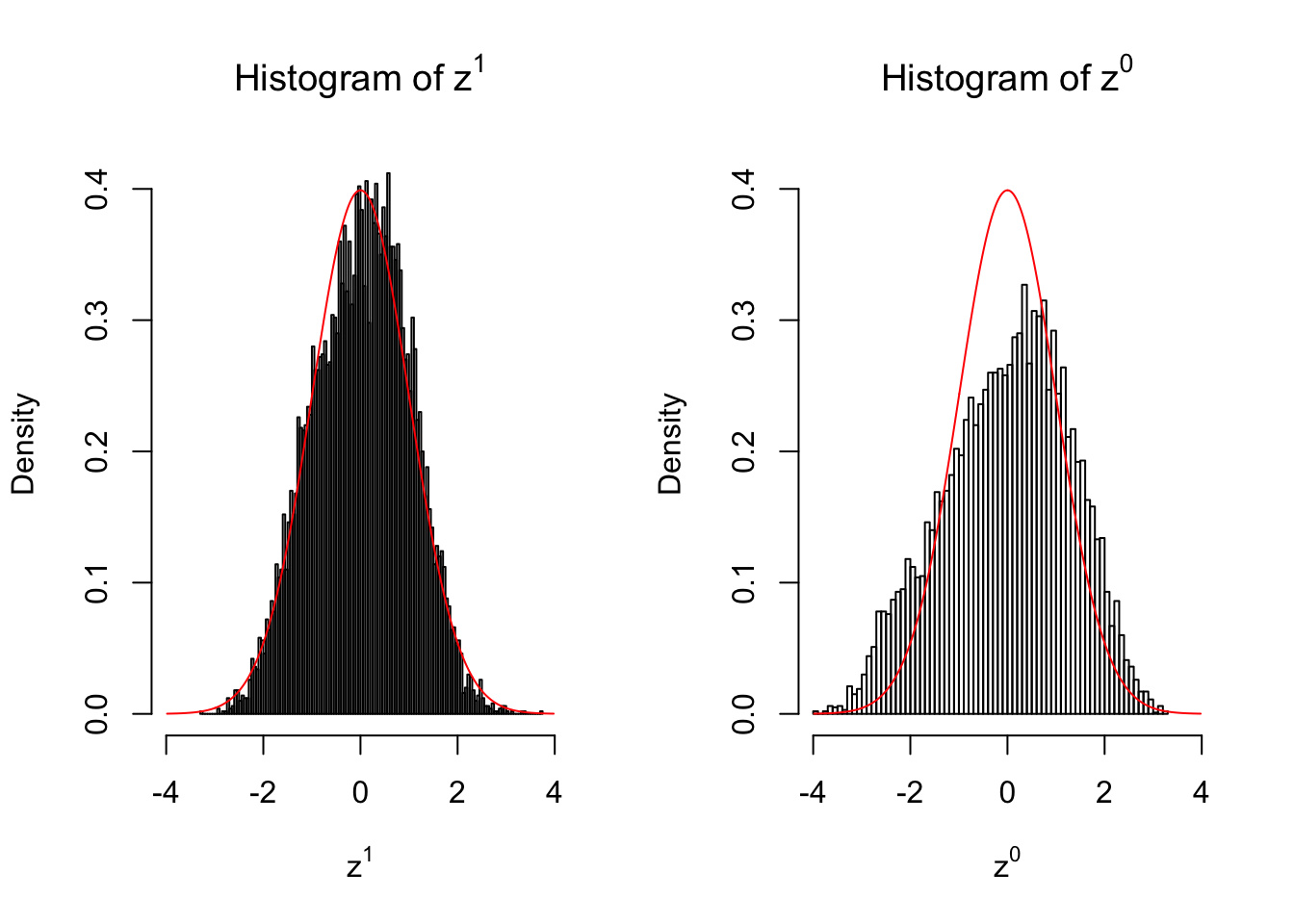
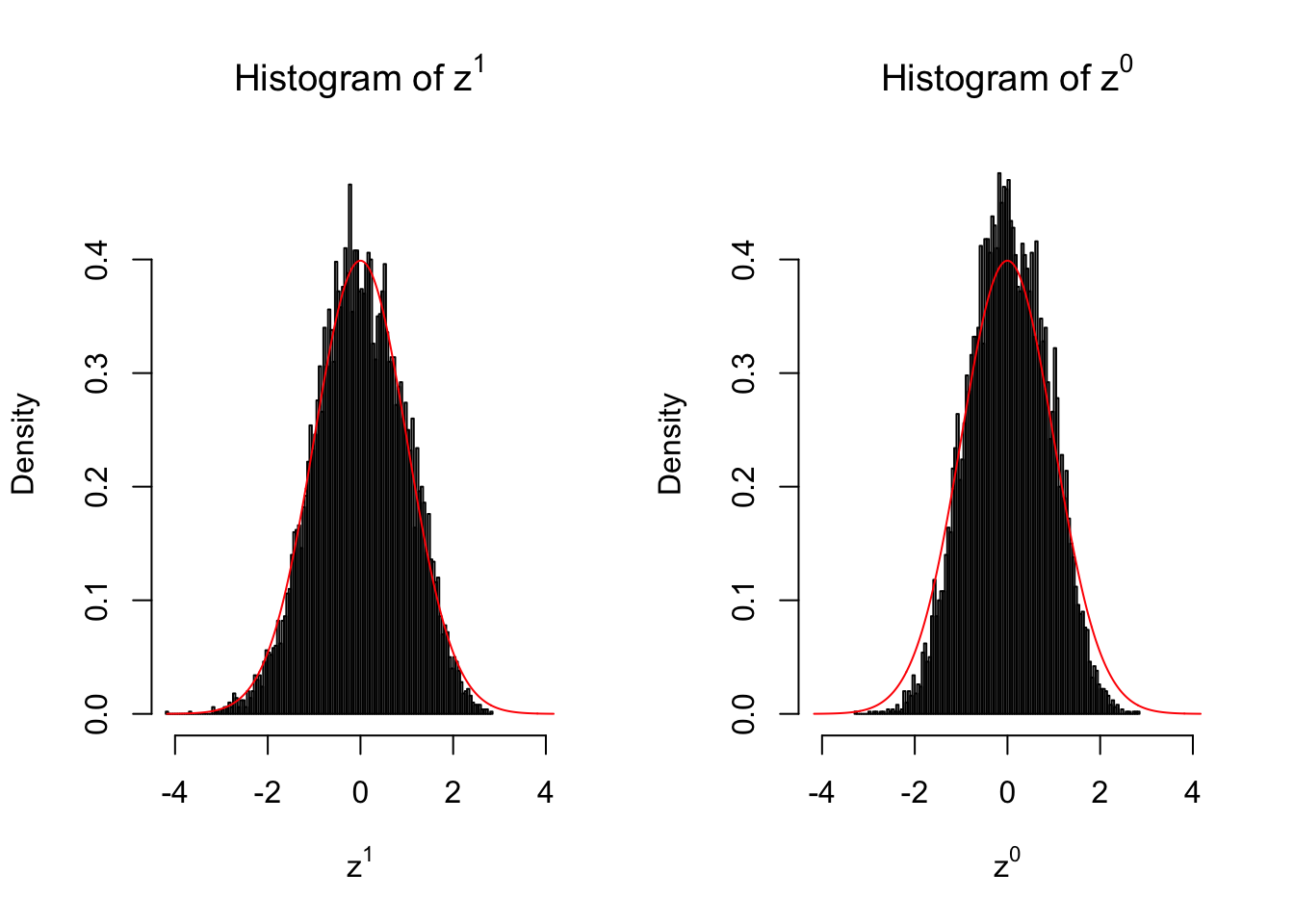
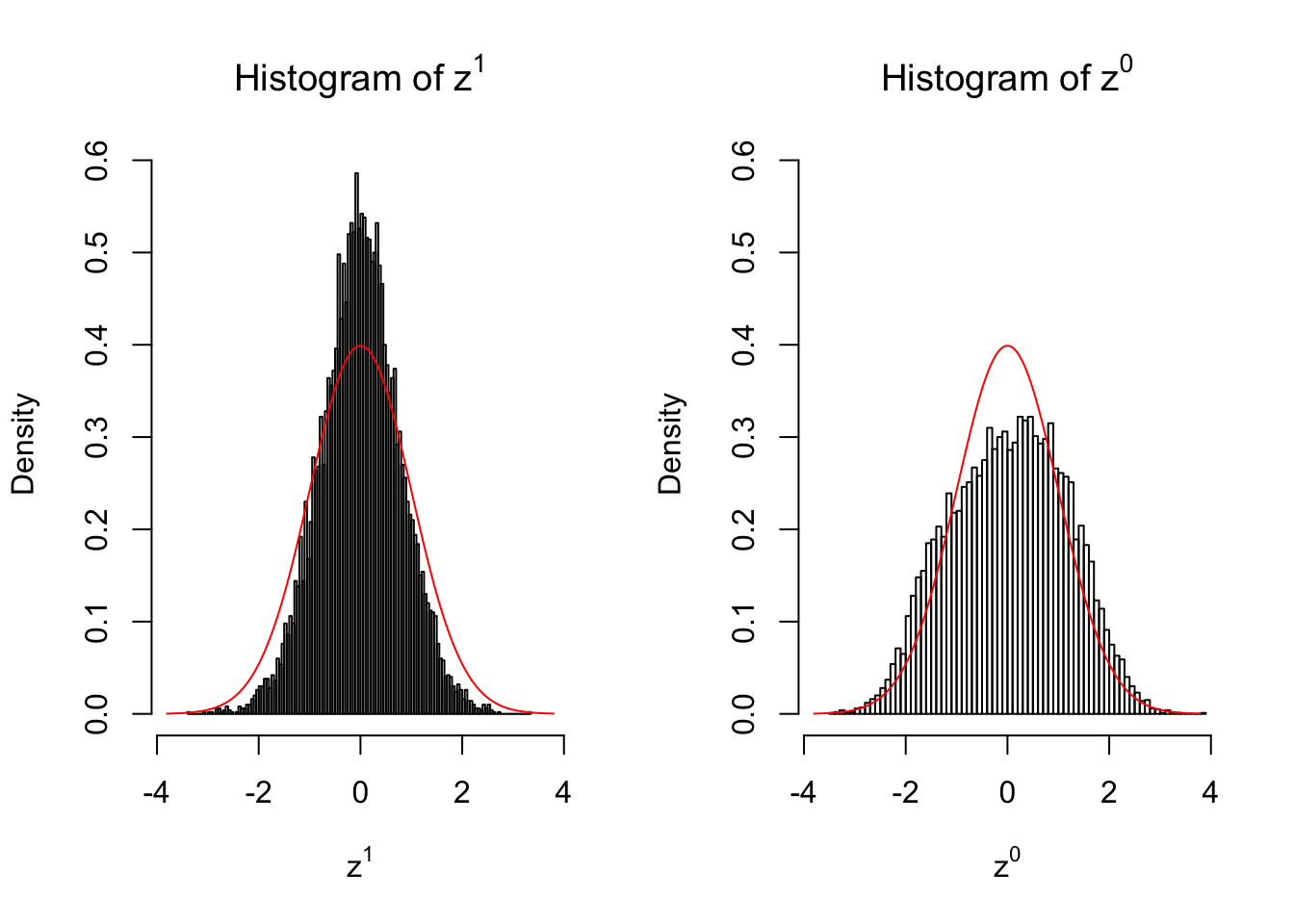
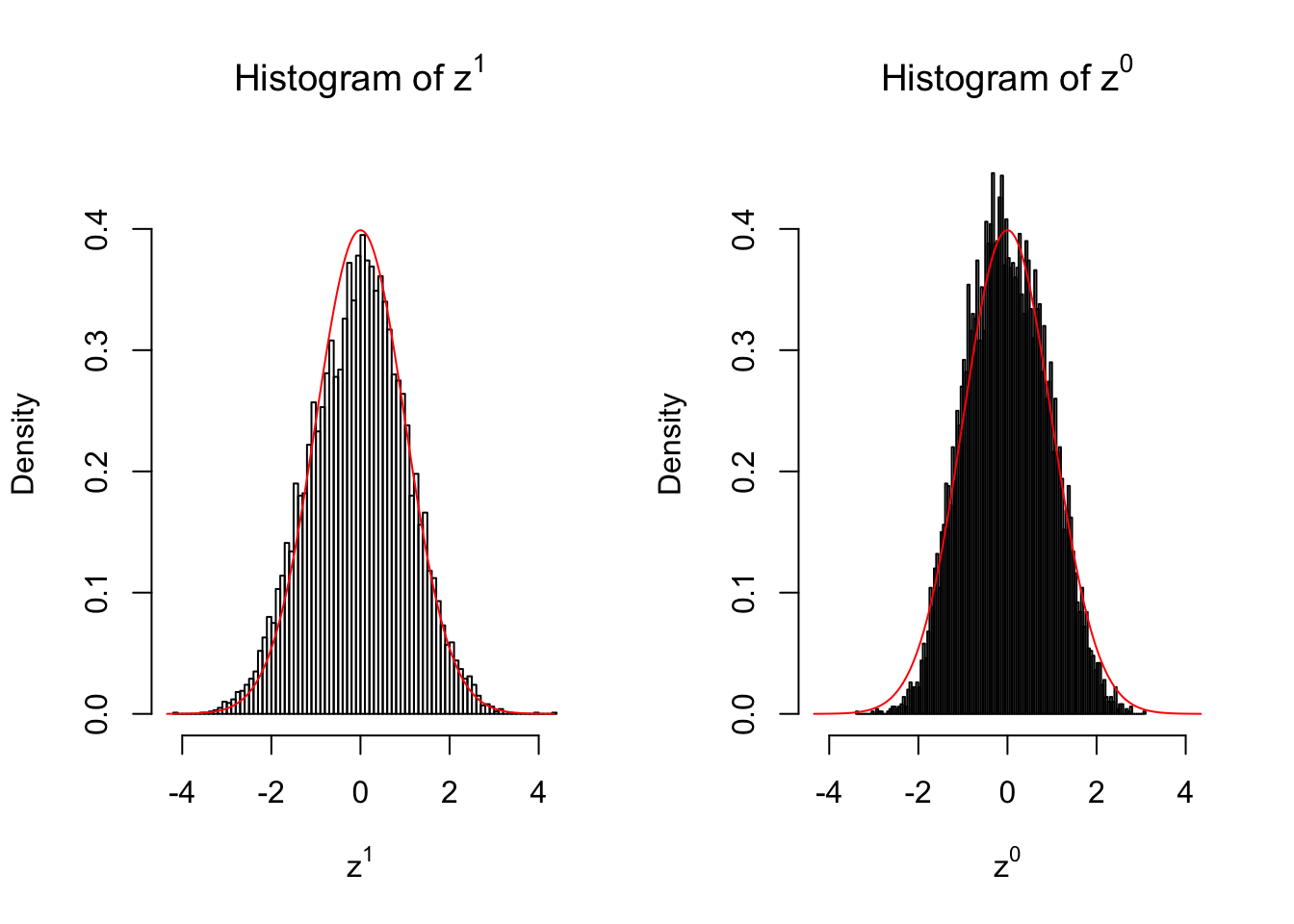
On the other hand, if we re-label case and control, and let \(\left\{X_1, \ldots, X_{n/2}, X_{n + 1}, \ldots, X_{3n / 2}\right\}\) be the controls and \(\left\{X_{n / 2 + 1}, \ldots, X_{n}, X_{3n / 2 + 1}, \ldots, X_{2n}\right\}\) the cases, we can obtain another \(N\) \(z\) scores, called \(z^0\), from this shuffled experimental design.
Our hope is that \(z^0\) will make the effects part in \(z^1\) to be \(0\), and only keep the correlation-induced inflation or deflation parts.
Here is a way to check this. Suppose there is no difference between the conditions in cases and controls, then the effects part in \(z^1\) should be \(0\) anyway. Therefore, we may check if \(z^0\) and \(z^1\) have the same empirical distribution distorted by correlation.
library(limma)
library(edgeR)
library(qvalue)
library(ashr)
r <- readRDS("../data/liver.rds")
ngene <- 1e4
top_genes_index = function (g, X) {
return(order(rowSums(X), decreasing = TRUE)[1 : g])
}
lcpm = function (r) {
R = colSums(r)
t(log2(((t(r) + 0.5) / (R + 1)) * 10^6))
}
Y = lcpm(r)
subset = top_genes_index(ngene, Y)
r = r[subset,]counts_to_z = function (counts, condition) {
design = stats::model.matrix(~condition)
dgecounts = edgeR::calcNormFactors(edgeR::DGEList(counts = counts, group = condition))
v = limma::voom(dgecounts, design, plot = FALSE)
lim = limma::lmFit(v)
r.ebayes = limma::eBayes(lim)
p = r.ebayes$p.value[, 2]
t = r.ebayes$t[, 2]
z = sign(t) * qnorm(1 - p/2)
return (z)
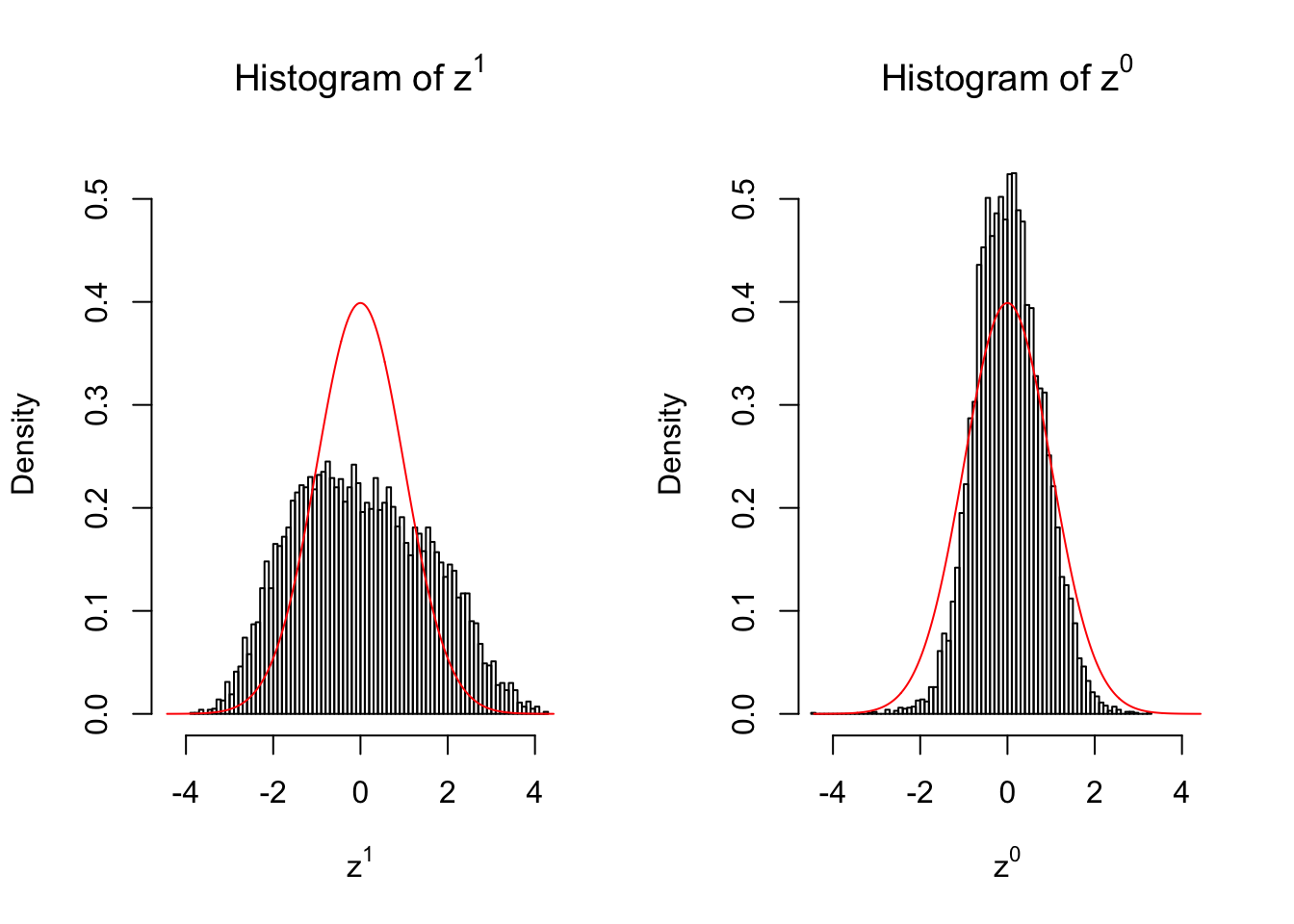
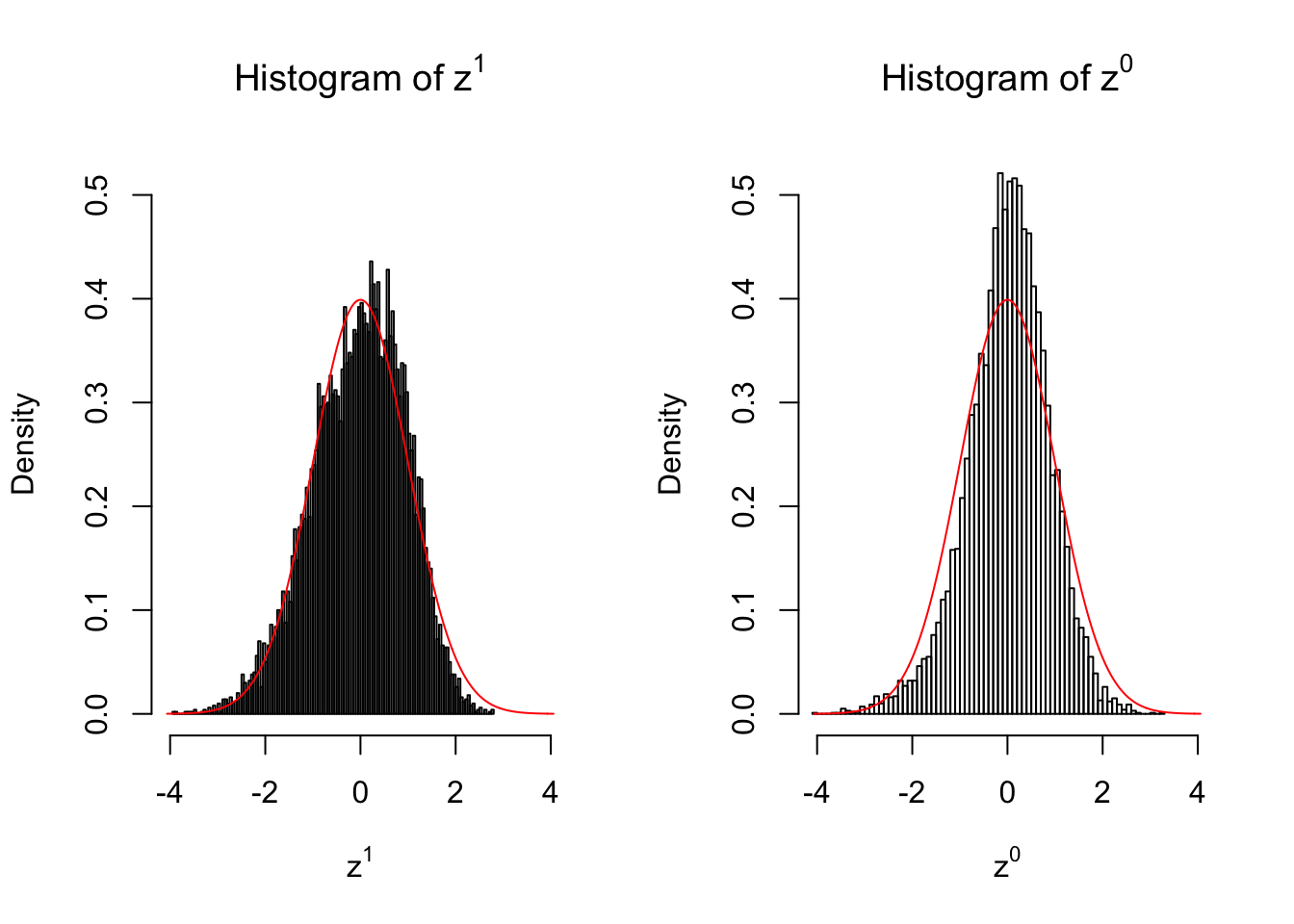
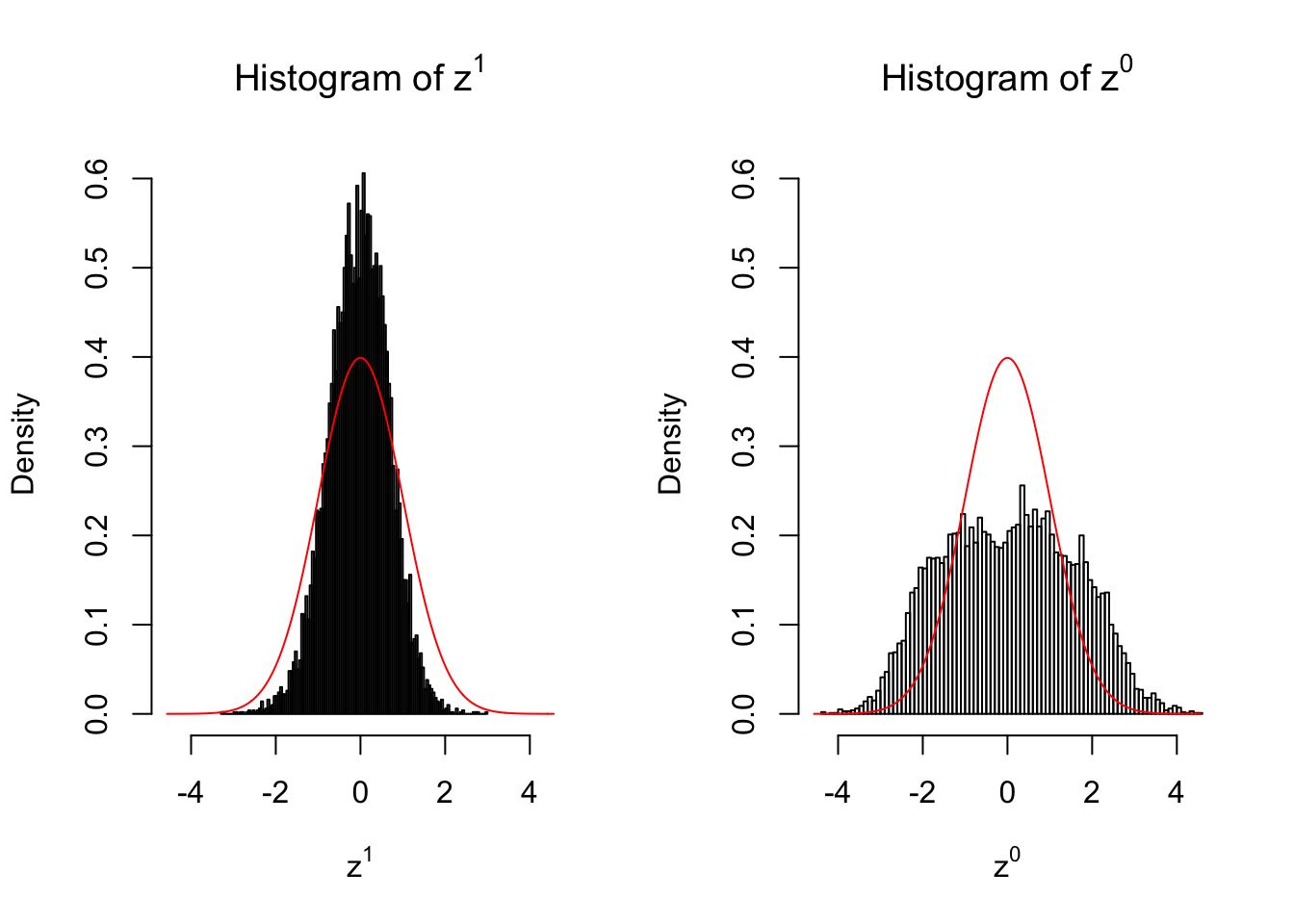
}We are looking at \(3\) cases with different case-control sample sizes: \(n = 2\), \(n = 10\), \(n = 50\).
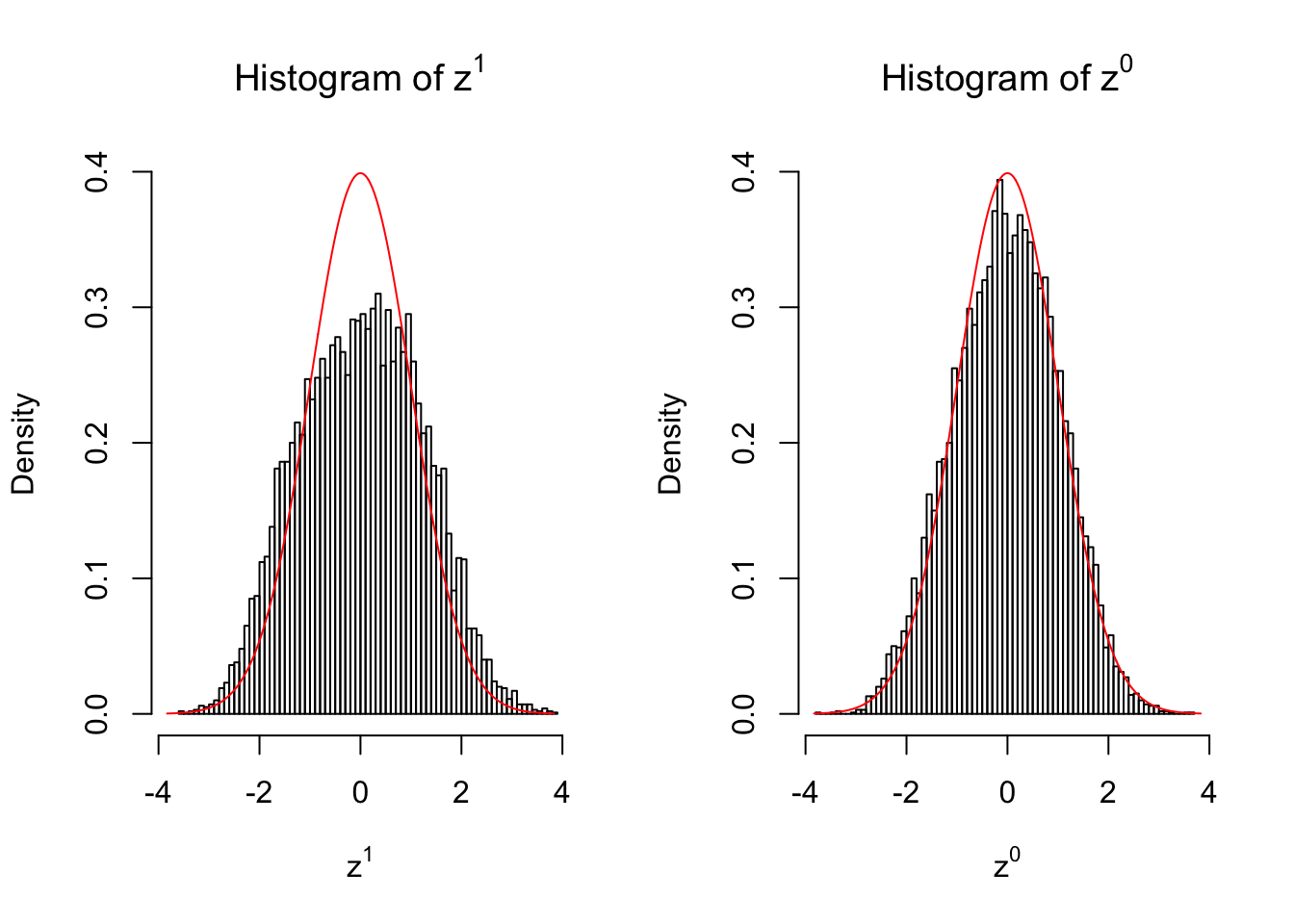
2 vs 2
set.seed(777)
n = 2
m = 10
z1 = z0 = list()
condition = c(rep(0, n), rep(1, n))
for (i in 1 : m) {
counts1 = r[, sample(ncol(r), 2 * n)]
counts0 = counts1[, c(seq(1, 2 * n, by = 2), seq(2, 2 * n, by = 2))]
z1[[i]] = counts_to_z(counts1, condition)
z0[[i]] = counts_to_z(counts0, condition)
}for (i in 1 : m) {
z1.hist = hist(z1[[i]], breaks = 100, plot = FALSE)
z0.hist = hist(z0[[i]], breaks = 100, plot = FALSE)
ymax = max(c(dnorm(0), z1.hist$density, z0.hist$density))
xmax = max(c(abs(z1[[i]]), abs(z0[[i]])))
par(mfrow = c(1, 2))
hist(z1[[i]], breaks = 100, prob = TRUE, xlab = expression(z^1), main = expression(paste("Histogram of ", z^1)), ylim = c(0, ymax), xlim = c(-xmax, xmax))
x.seq = seq(-xmax, xmax, 0.01)
lines(x.seq, dnorm(x.seq), col = "red")
hist(z0[[i]], breaks = 100, prob = TRUE, xlab = expression(z^0), main = expression(paste("Histogram of ", z^0)), ylim = c(0, ymax), xlim = c(-xmax, xmax))
lines(x.seq, dnorm(x.seq), col = "red")
}
Expand here to see past versions of unnamed-chunk-4-1.png:
| Version | Author | Date |
|---|---|---|
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-4-2.png:
| Version | Author | Date |
|---|---|---|
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-4-3.png:
| Version | Author | Date |
|---|---|---|
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-4-4.png:
| Version | Author | Date |
|---|---|---|
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-4-5.png:
| Version | Author | Date |
|---|---|---|
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-4-6.png:
| Version | Author | Date |
|---|---|---|
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-4-7.png:
| Version | Author | Date |
|---|---|---|
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-4-8.png:
| Version | Author | Date |
|---|---|---|
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-4-9.png:
| Version | Author | Date |
|---|---|---|
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-4-10.png:
| Version | Author | Date |
|---|---|---|
| b141020 | LSun | 2017-05-09 |
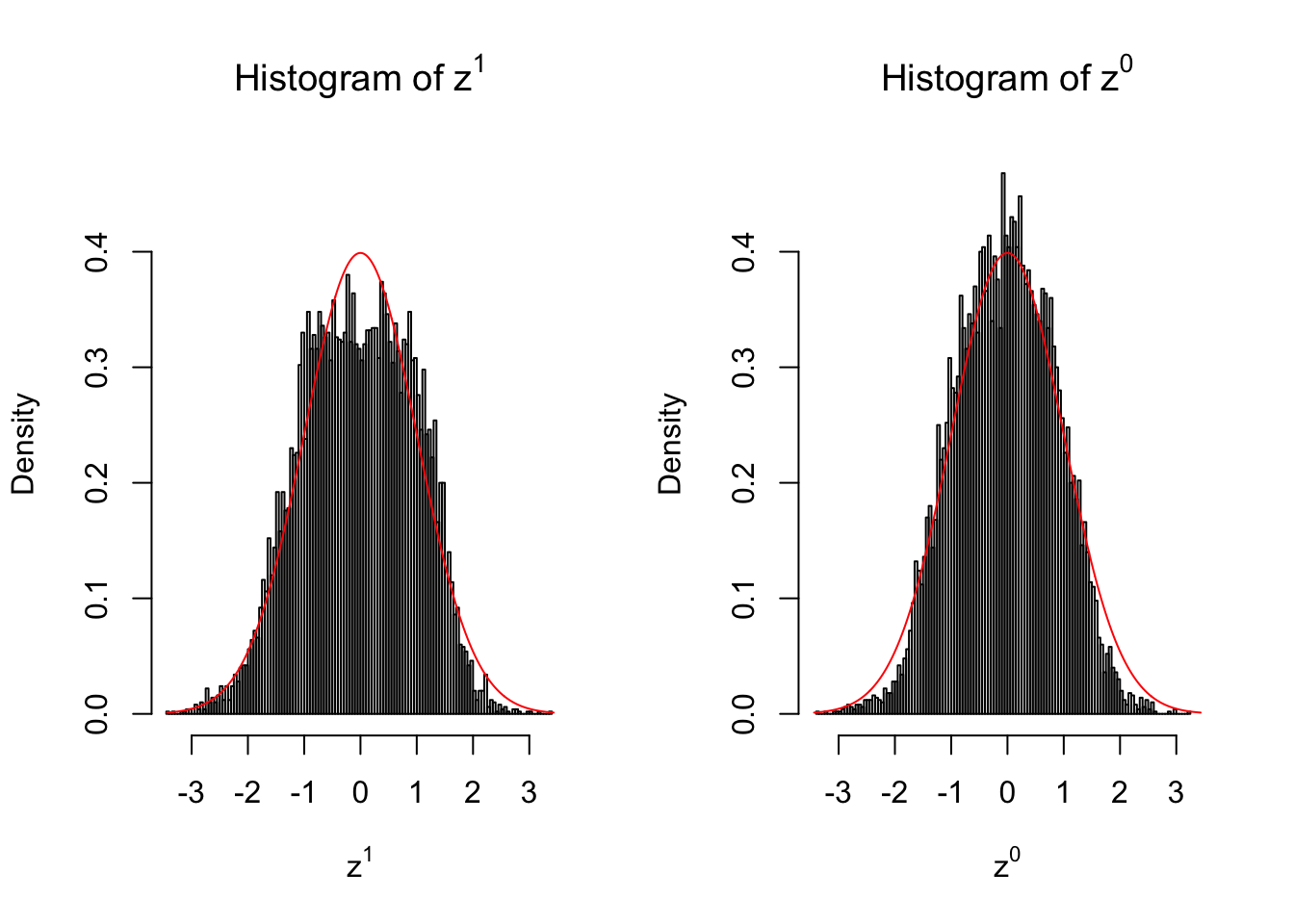
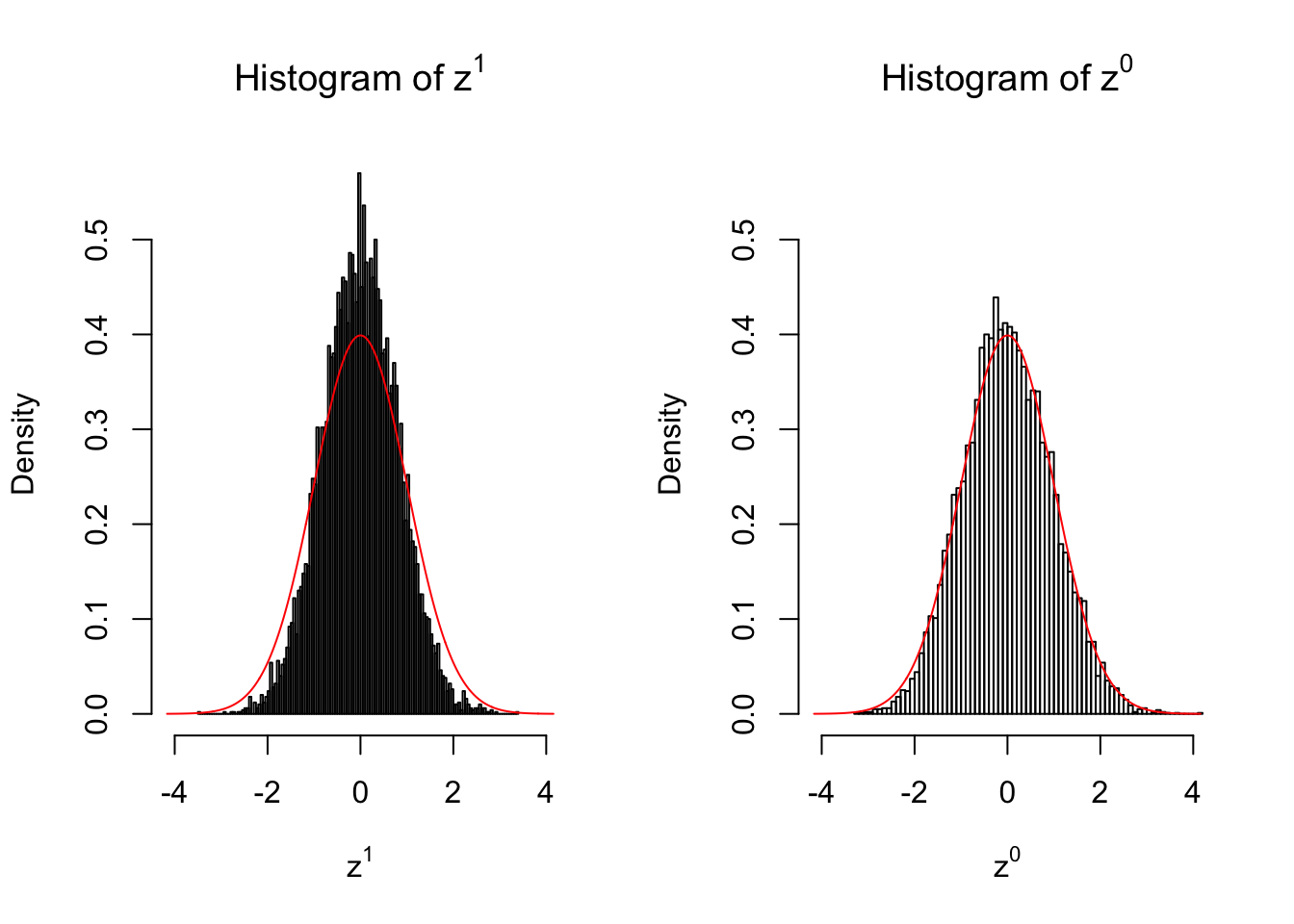
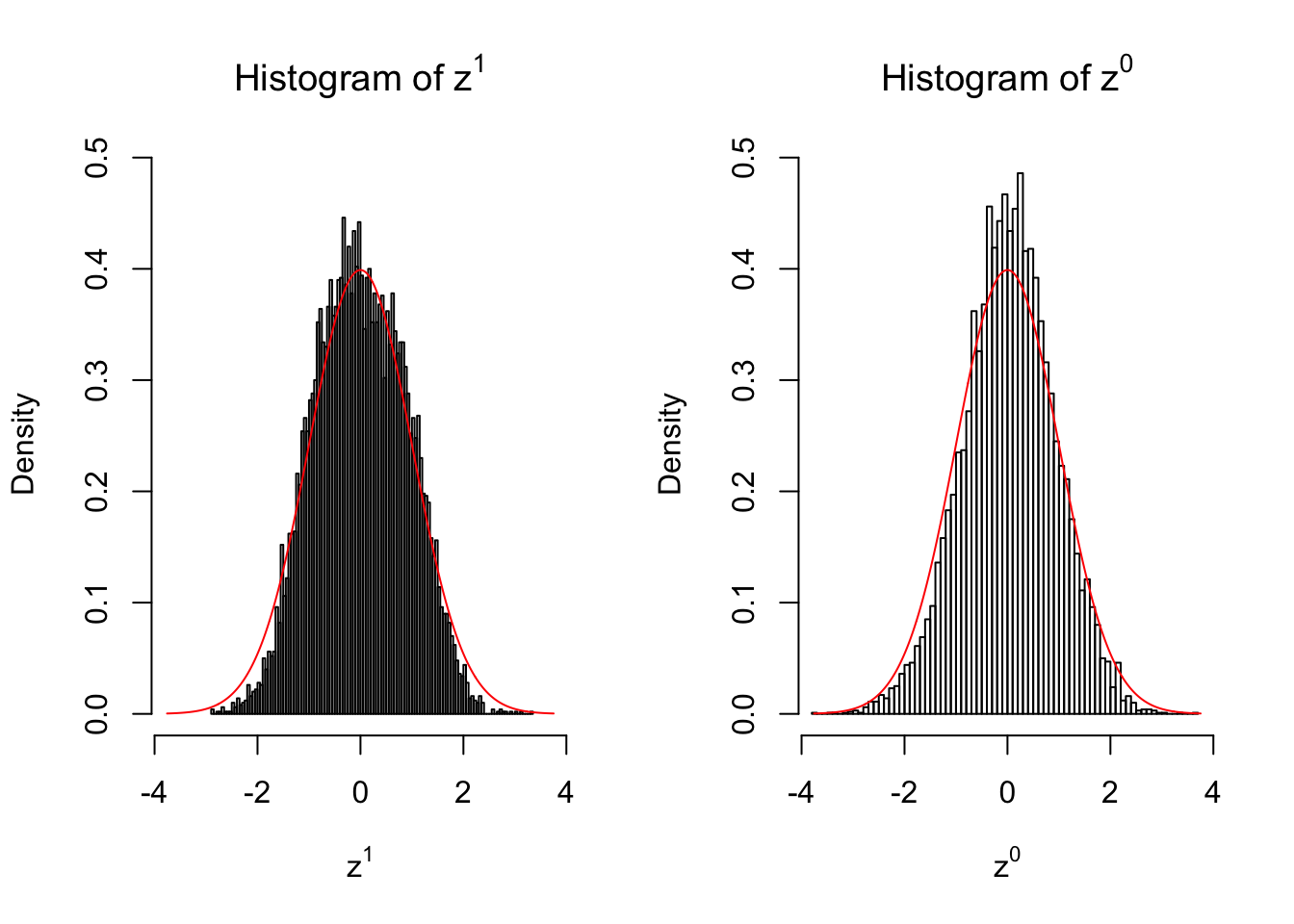
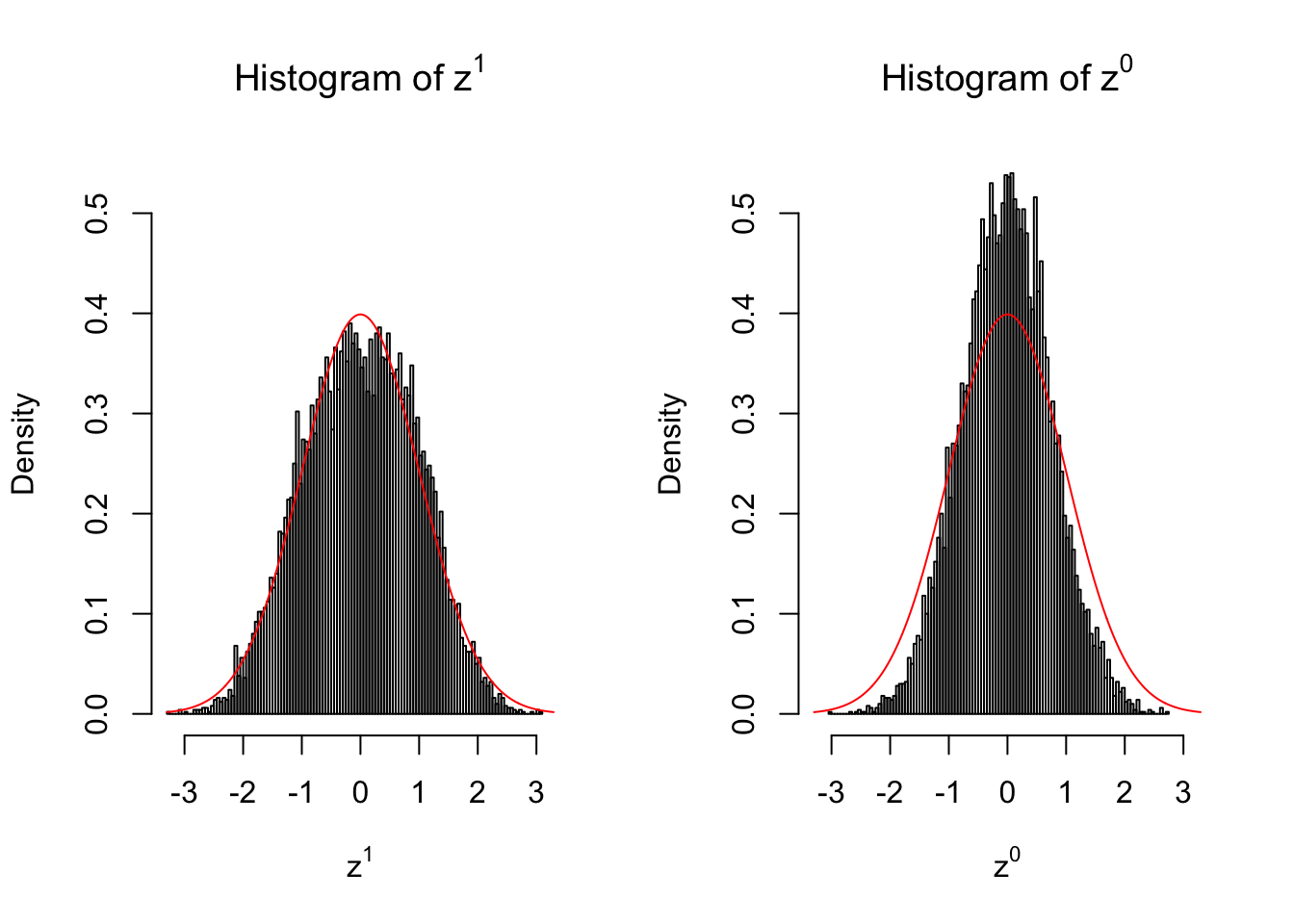
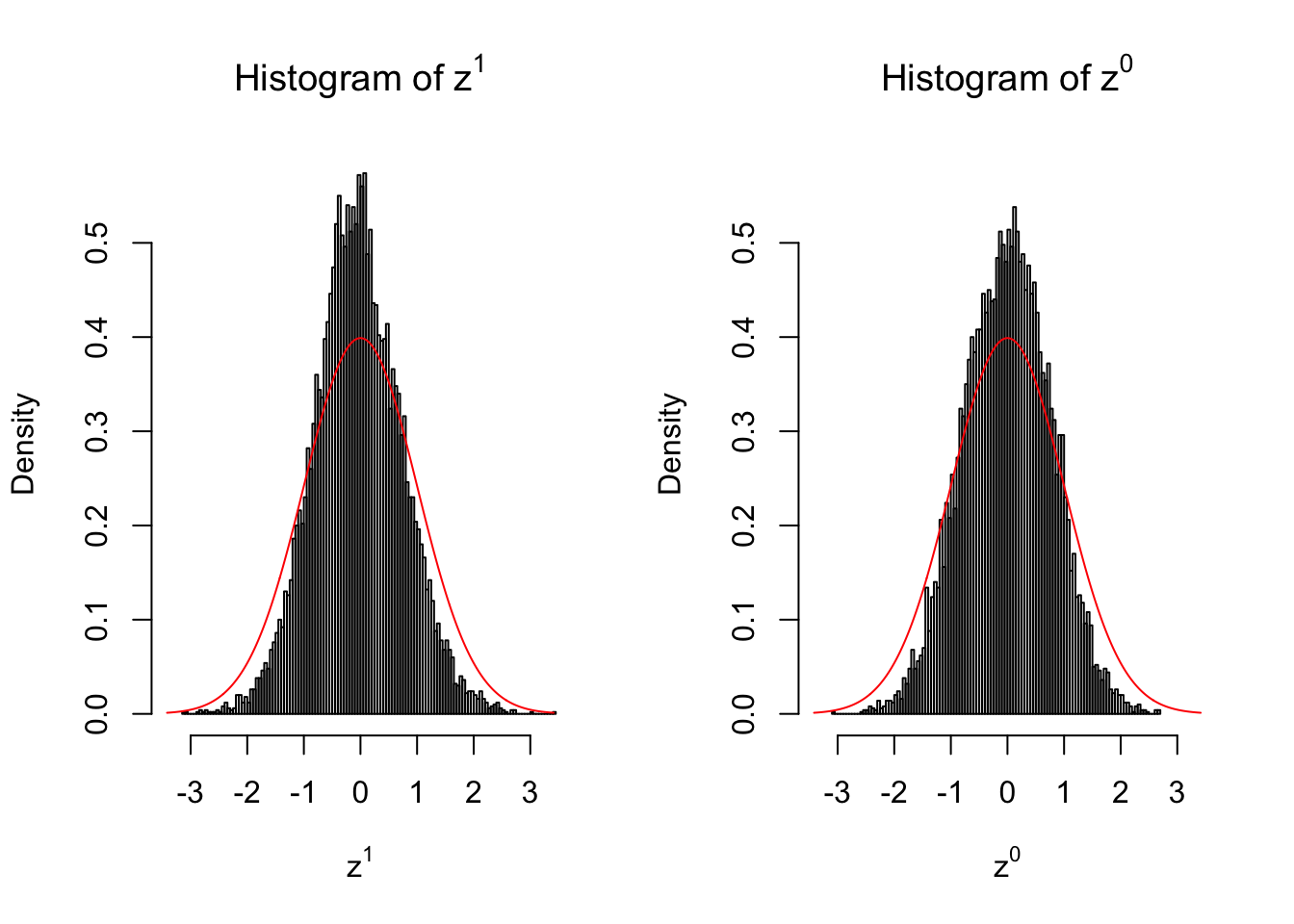
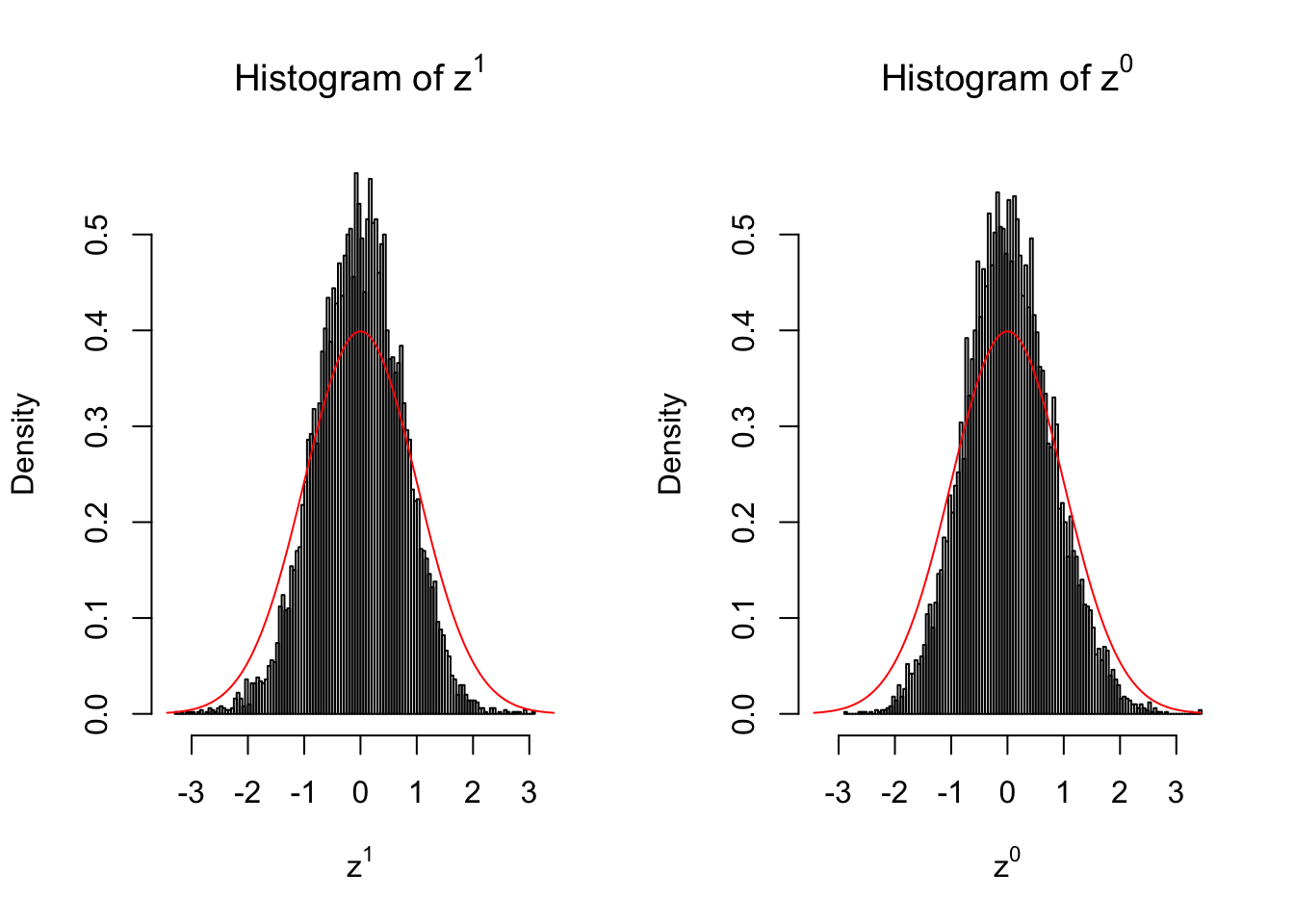
10 vs 10
set.seed(777)
n = 10
m = 10
z1 = z0 = list()
condition = c(rep(0, n), rep(1, n))
for (i in 1 : m) {
counts1 = r[, sample(1 : ncol(r), 2 * n)]
counts0 = counts1[, c(seq(1, 2 * n, by = 2), seq(2, 2 * n, by = 2))]
z1[[i]] = counts_to_z(counts1, condition)
z0[[i]] = counts_to_z(counts0, condition)
}for (i in 1 : m) {
z1.hist = hist(z1[[i]], breaks = 100, plot = FALSE)
z0.hist = hist(z0[[i]], breaks = 100, plot = FALSE)
ymax = max(c(dnorm(0), z1.hist$density, z0.hist$density))
xmax = max(c(abs(z1[[i]]), abs(z0[[i]])))
par(mfrow = c(1, 2))
hist(z1[[i]], breaks = 100, prob = TRUE, xlab = expression(z^1), main = expression(paste("Histogram of ", z^1)), ylim = c(0, ymax), xlim = c(-xmax, xmax))
x.seq = seq(-xmax, xmax, 0.01)
lines(x.seq, dnorm(x.seq), col = "red")
hist(z0[[i]], breaks = 100, prob = TRUE, xlab = expression(z^0), main = expression(paste("Histogram of ", z^0)), ylim = c(0, ymax), xlim = c(-xmax, xmax))
lines(x.seq, dnorm(x.seq), col = "red")
}
Expand here to see past versions of unnamed-chunk-6-1.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-6-2.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-6-3.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-6-4.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-6-5.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-6-6.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-6-7.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-6-8.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-6-9.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
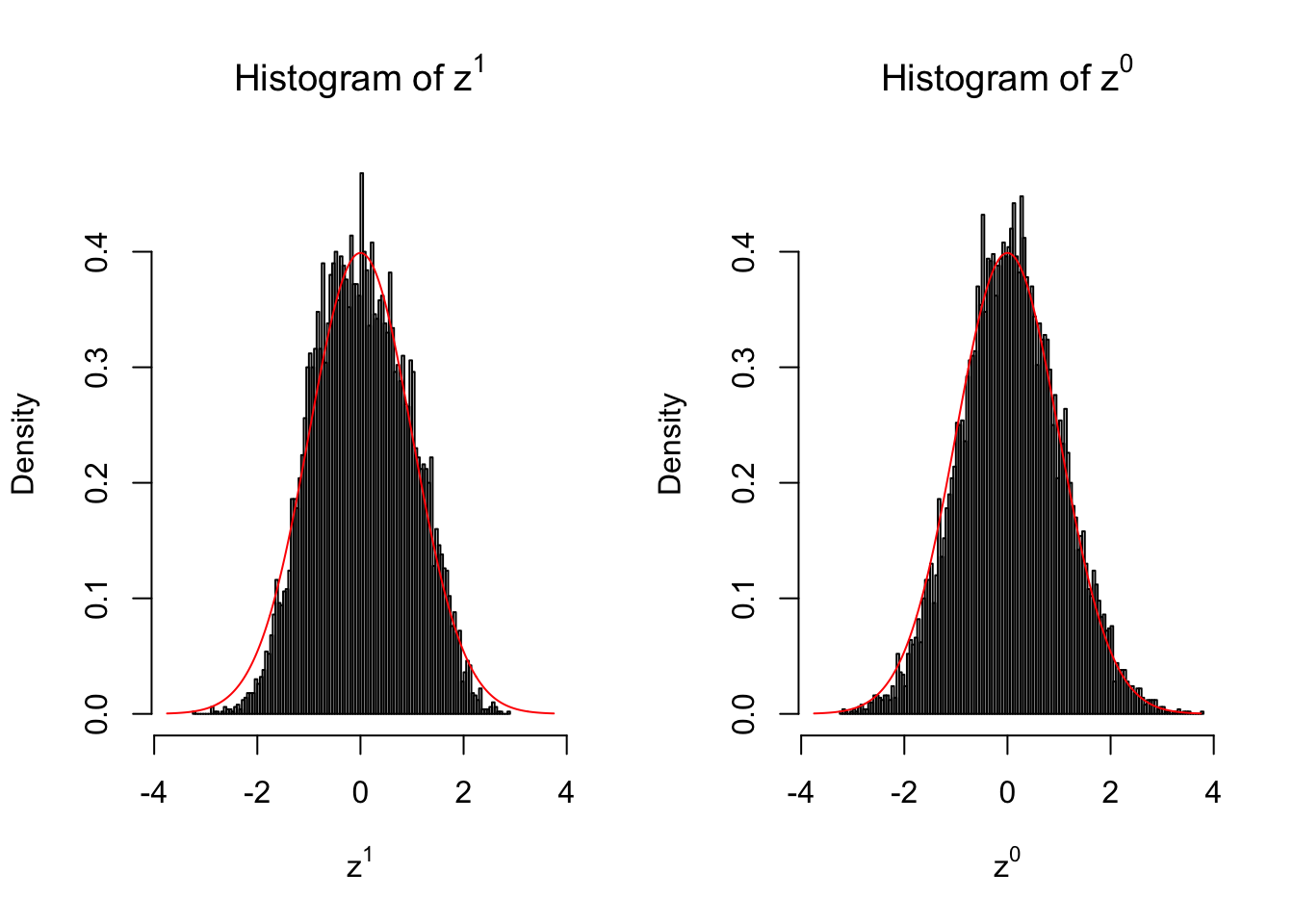
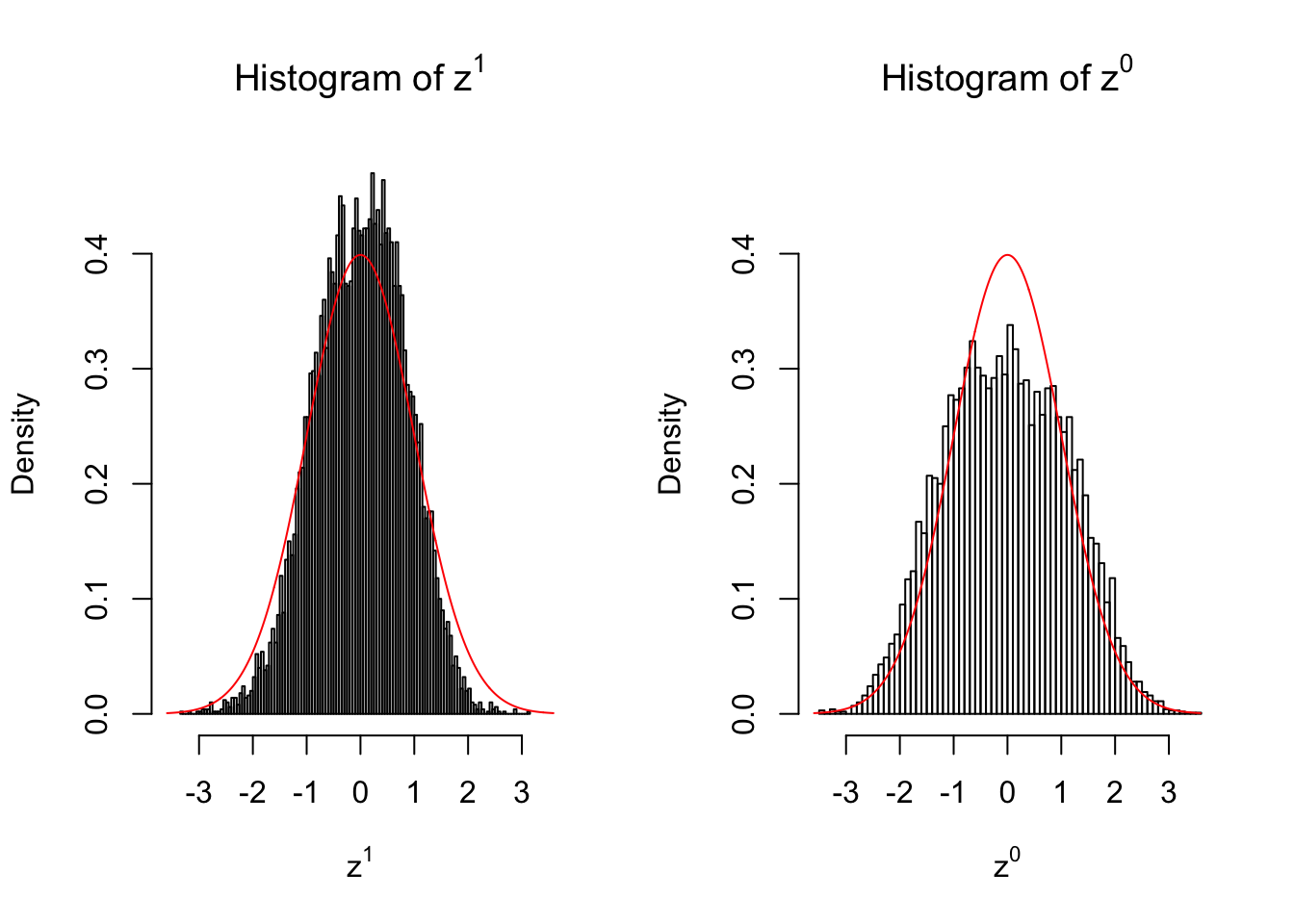
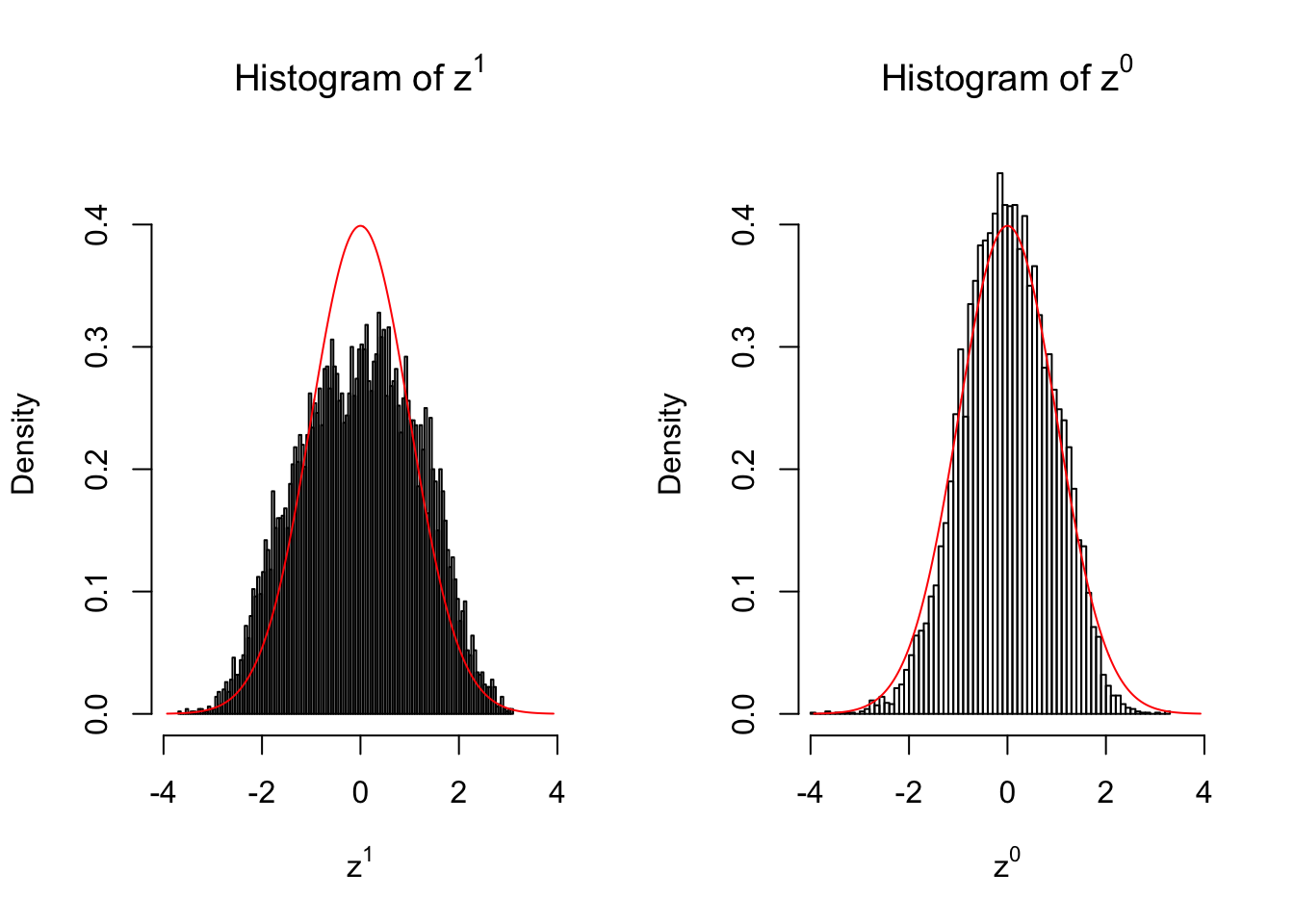
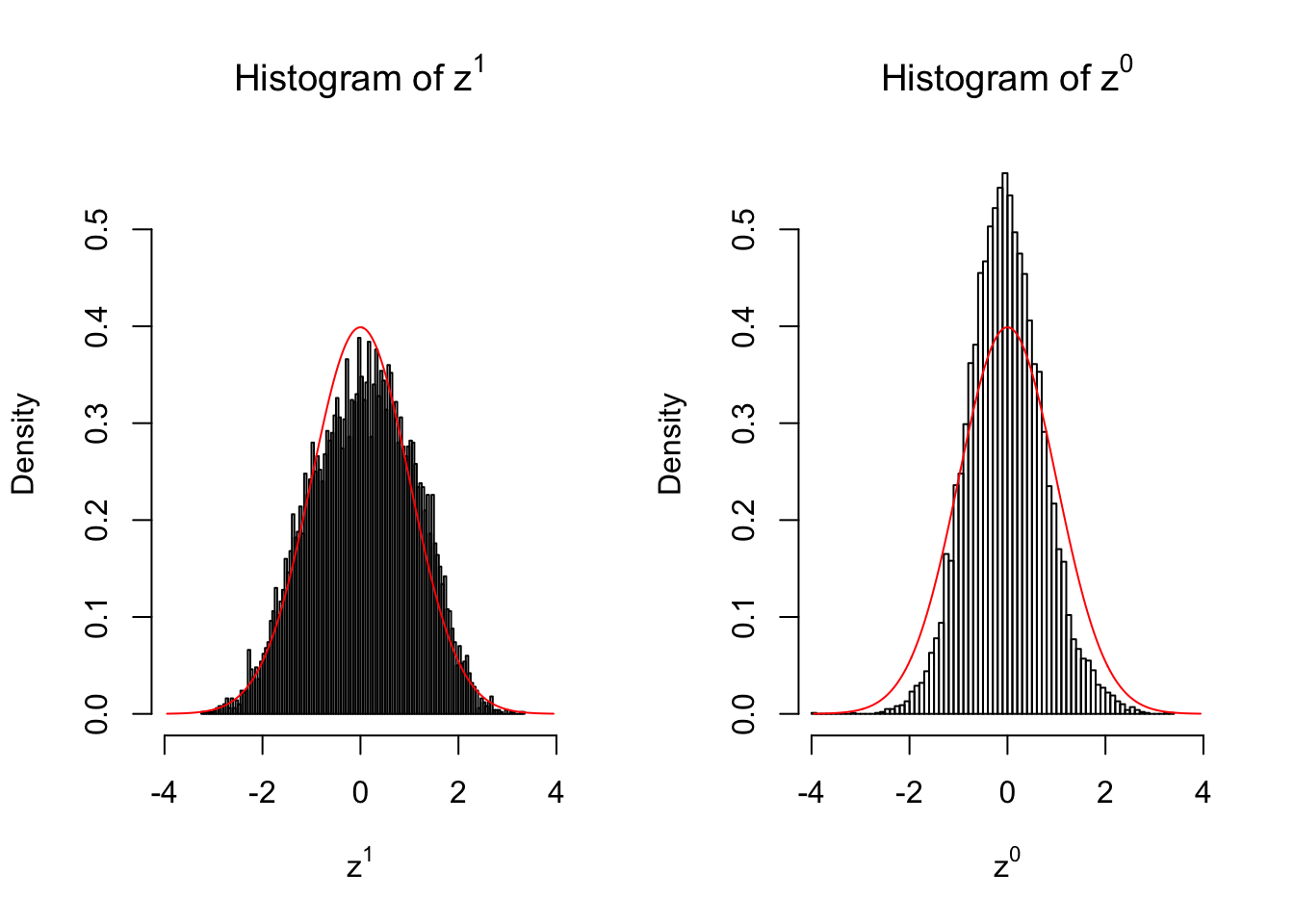
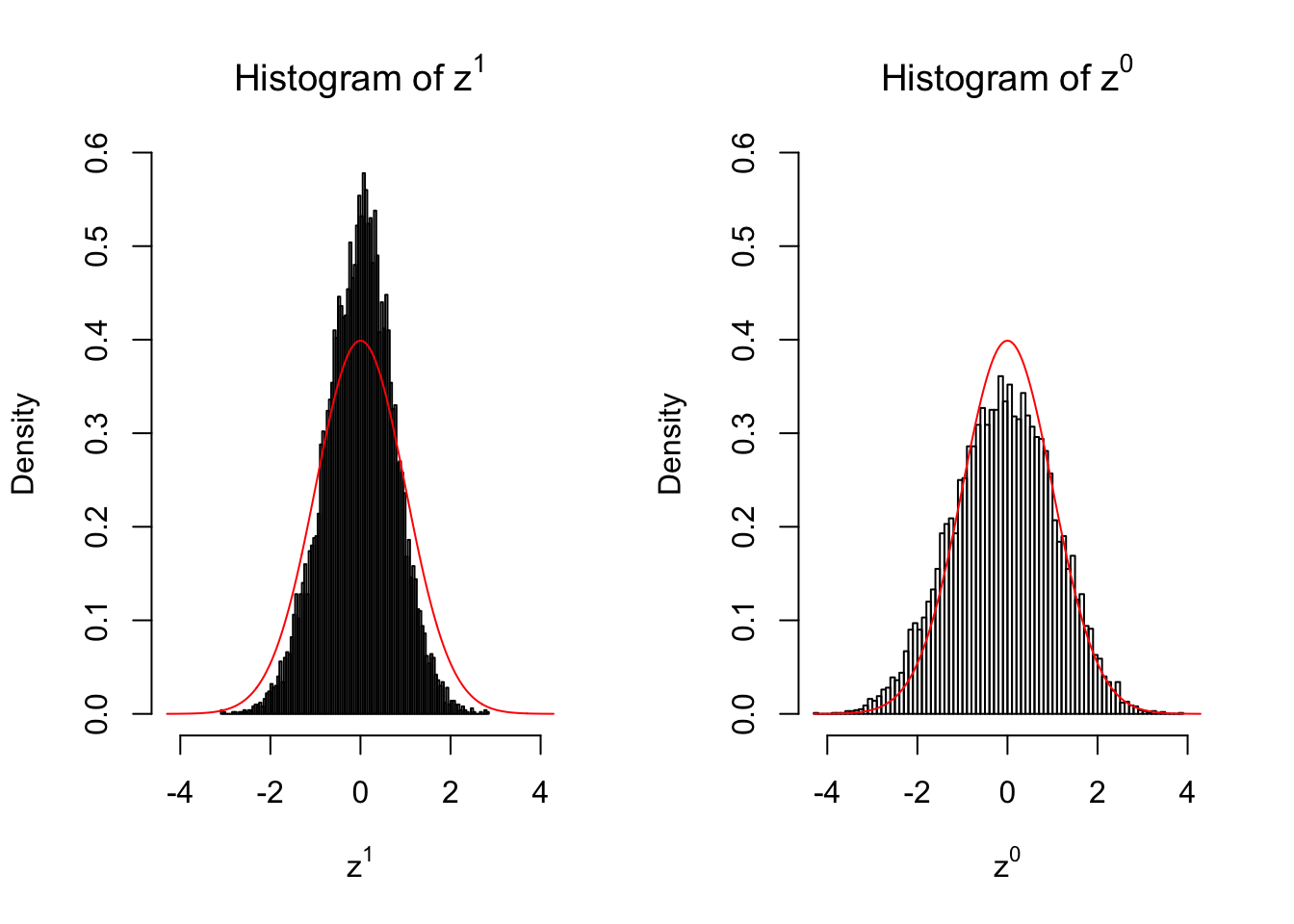
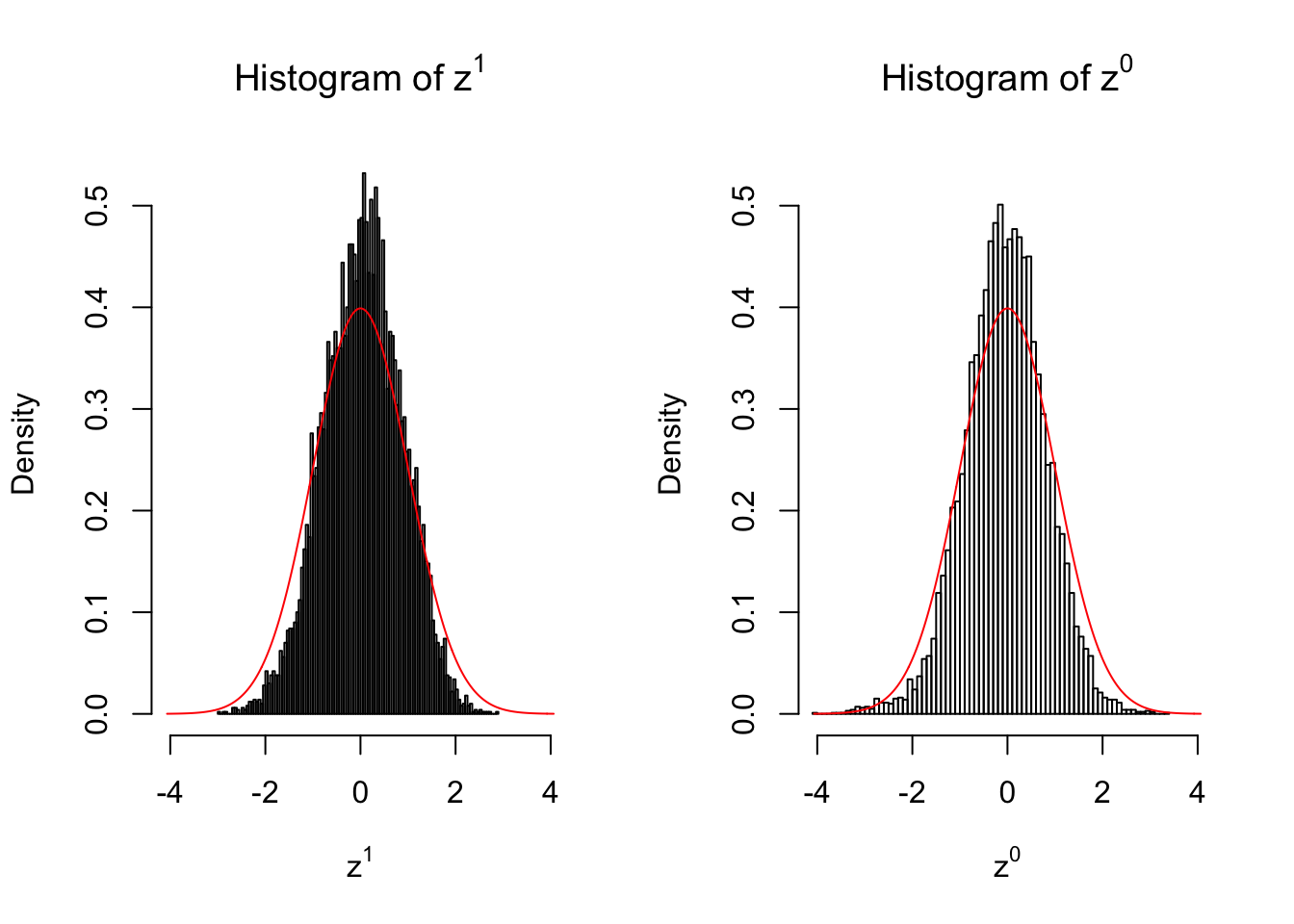
50 vs 50
set.seed(777)
n = 50
m = 10
z1 = z0 = list()
condition = c(rep(0, n), rep(1, n))
for (i in 1 : m) {
counts1 = r[, sample(1 : ncol(r), 2 * n)]
counts0 = counts1[, c(seq(1, 2 * n, by = 2), seq(2, 2 * n, by = 2))]
z1[[i]] = counts_to_z(counts1, condition)
z0[[i]] = counts_to_z(counts0, condition)
}for (i in 1 : m) {
z1.hist = hist(z1[[i]], breaks = 100, plot = FALSE)
z0.hist = hist(z0[[i]], breaks = 100, plot = FALSE)
ymax = max(c(dnorm(0), z1.hist$density, z0.hist$density))
xmax = max(c(abs(z1[[i]]), abs(z0[[i]])))
par(mfrow = c(1, 2))
hist(z1[[i]], breaks = 100, prob = TRUE, xlab = expression(z^1), main = expression(paste("Histogram of ", z^1)), ylim = c(0, ymax), xlim = c(-xmax, xmax))
x.seq = seq(-xmax, xmax, 0.01)
lines(x.seq, dnorm(x.seq), col = "red")
hist(z0[[i]], breaks = 100, prob = TRUE, xlab = expression(z^0), main = expression(paste("Histogram of ", z^0)), ylim = c(0, ymax), xlim = c(-xmax, xmax))
lines(x.seq, dnorm(x.seq), col = "red")
}
Expand here to see past versions of unnamed-chunk-8-1.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-8-2.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-8-3.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
Expand here to see past versions of unnamed-chunk-8-4.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
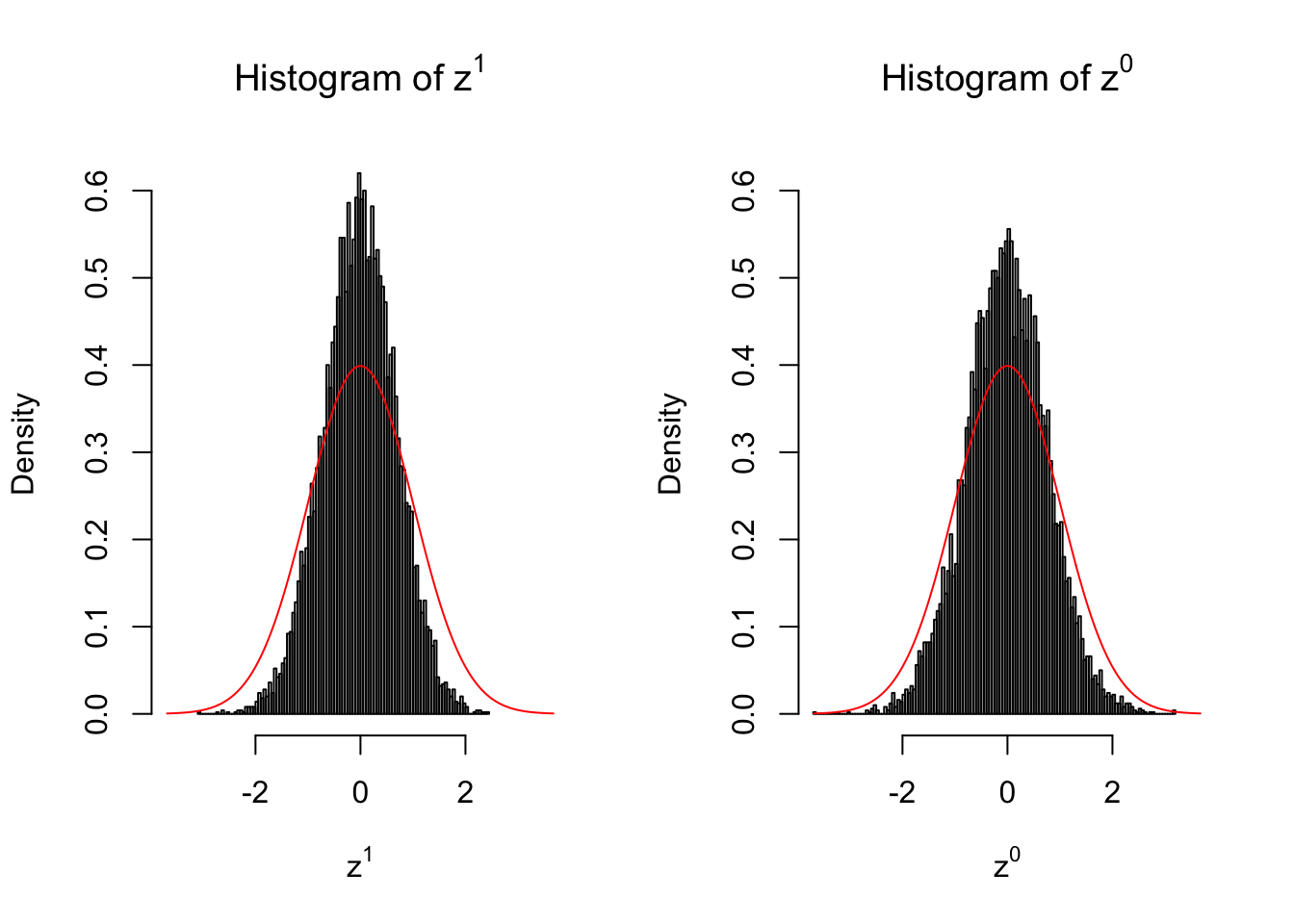
Expand here to see past versions of unnamed-chunk-8-5.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
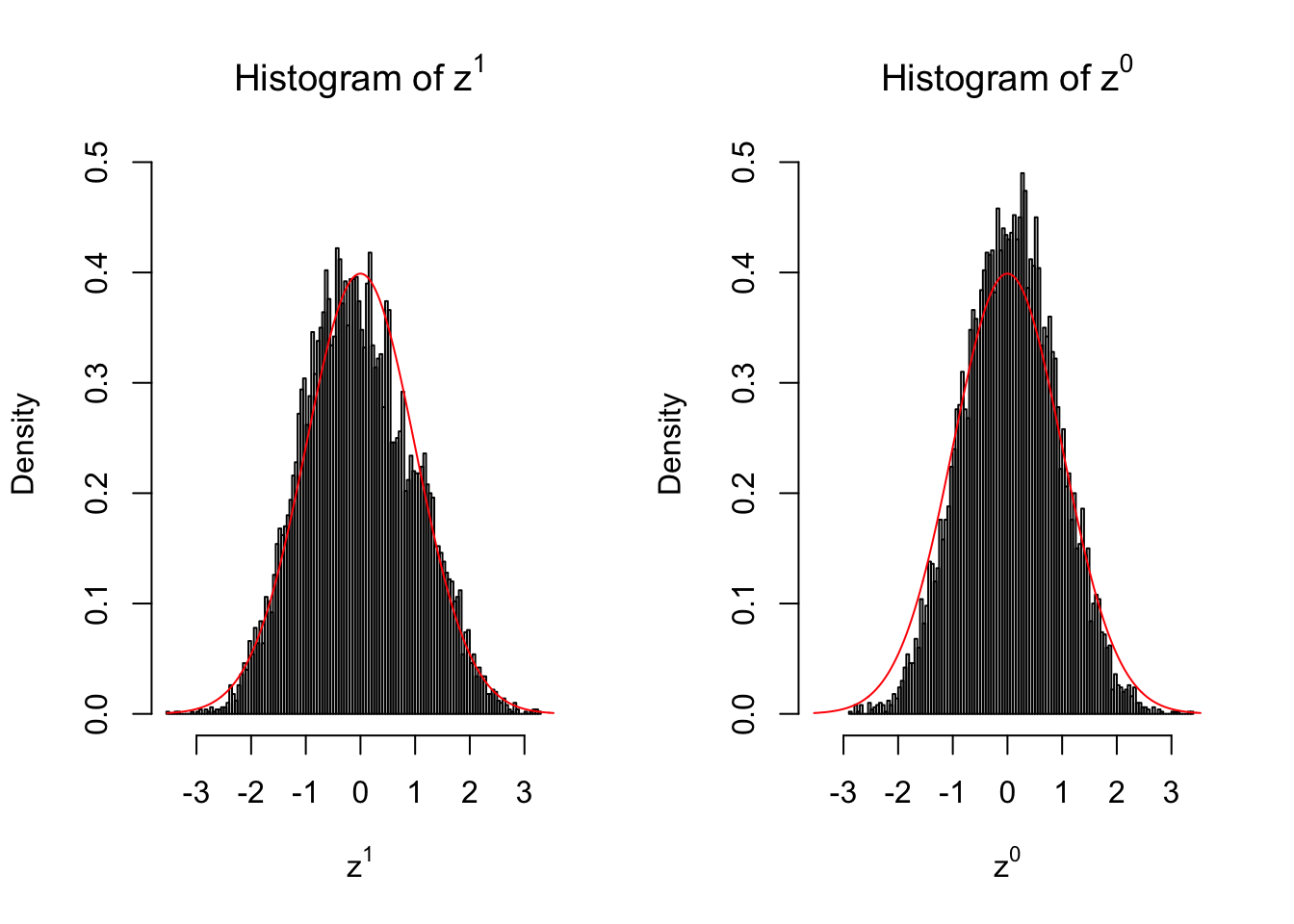
Expand here to see past versions of unnamed-chunk-8-6.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
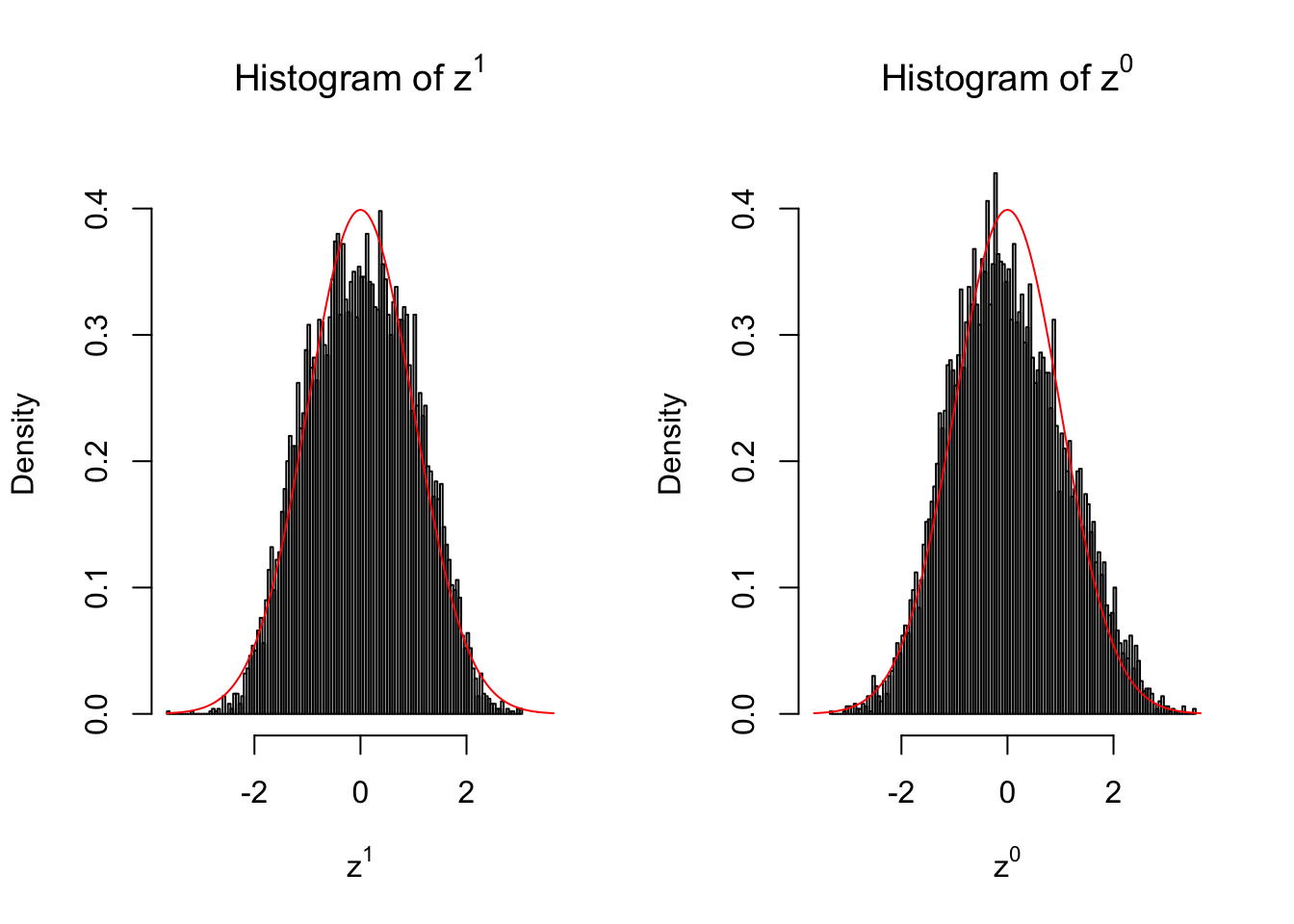
Expand here to see past versions of unnamed-chunk-8-7.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
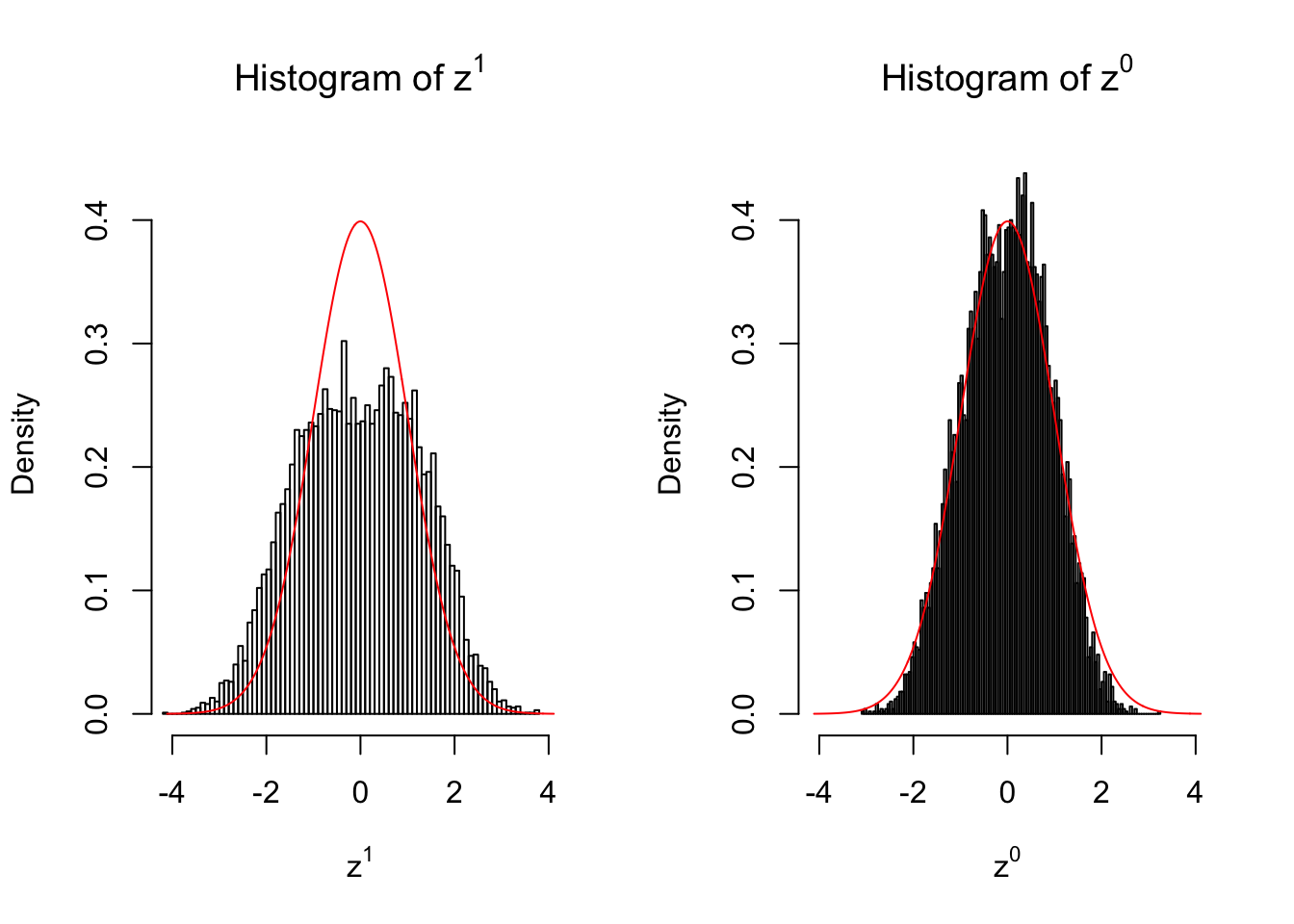
Expand here to see past versions of unnamed-chunk-8-8.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
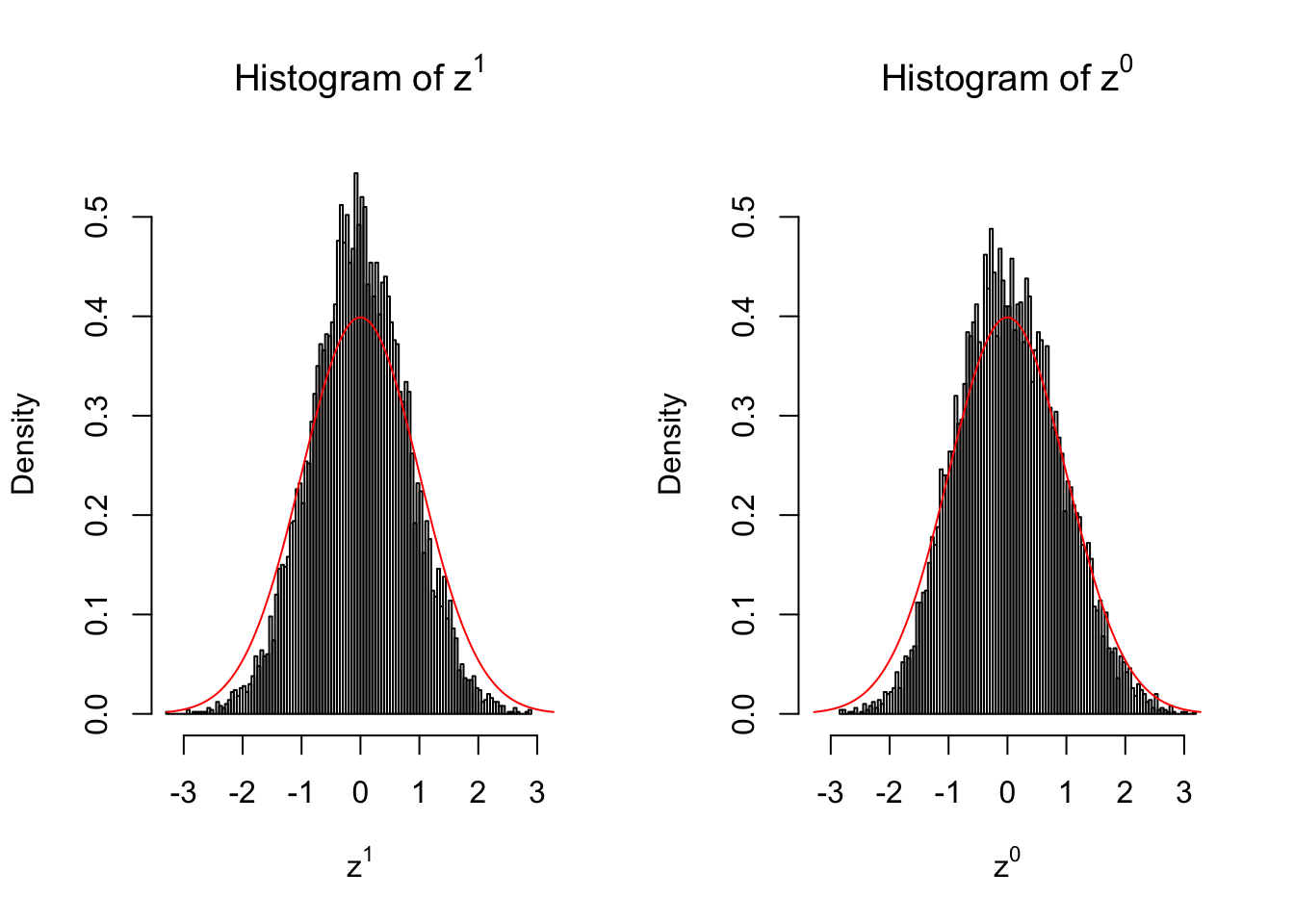
Expand here to see past versions of unnamed-chunk-8-9.png:
| Version | Author | Date |
|---|---|---|
| b8d63a5 | LSun | 2018-06-01 |
| b141020 | LSun | 2017-05-09 |
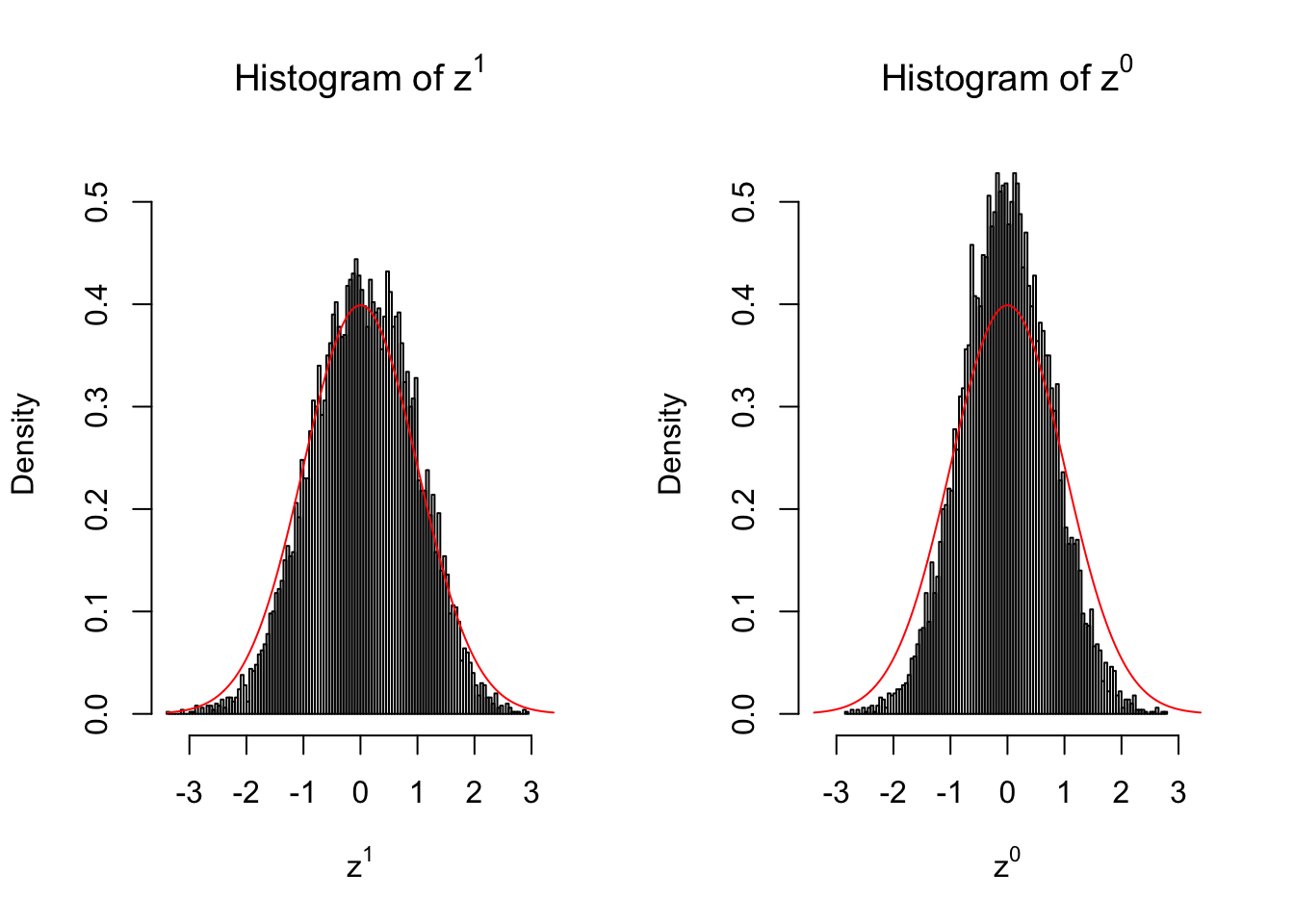
Conclusion
Larger sample size doesn’t make the empirical distribution of correlated \(z\) scores closer to \(N\left(0, 1\right)\).
Merely changing the labels of the null data could generate starkly different empirical distributions of \(z\) scores, no matter what sample size \(n\) is, although as \(n\) gets larger, the difference in the empirical distributions of \(z^1\) and \(z^0\) seems to get smaller.
Therefore, creating null through various resampling schemes is basically impossible for this application.
Session information
sessionInfo()R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.4
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] ashr_2.2-7 qvalue_2.10.0 edgeR_3.20.9 limma_3.34.9
loaded via a namespace (and not attached):
[1] Rcpp_0.12.16 compiler_3.4.3 pillar_1.2.2
[4] git2r_0.21.0 plyr_1.8.4 workflowr_1.0.1
[7] iterators_1.0.9 R.methodsS3_1.7.1 R.utils_2.6.0
[10] tools_3.4.3 digest_0.6.15 evaluate_0.10.1
[13] tibble_1.4.2 gtable_0.2.0 lattice_0.20-35
[16] rlang_0.2.0 foreach_1.4.4 Matrix_1.2-14
[19] parallel_3.4.3 yaml_2.1.19 stringr_1.3.1
[22] knitr_1.20 locfit_1.5-9.1 rprojroot_1.3-2
[25] grid_3.4.3 rmarkdown_1.9 ggplot2_2.2.1
[28] reshape2_1.4.3 magrittr_1.5 whisker_0.3-2
[31] MASS_7.3-50 codetools_0.2-15 backports_1.1.2
[34] scales_0.5.0 htmltools_0.3.6 splines_3.4.3
[37] colorspace_1.3-2 stringi_1.2.2 pscl_1.5.2
[40] lazyeval_0.2.1 munsell_0.4.3 doParallel_1.0.11
[43] truncnorm_1.0-8 SQUAREM_2017.10-1 R.oo_1.22.0 This reproducible R Markdown analysis was created with workflowr 1.0.1